题目内容
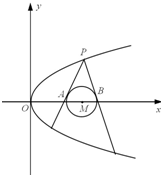 (2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为
(2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为| 9 |
| 2 |
(Ⅰ)求抛物线C的方程;
(Ⅱ)当P点坐标为(2,2)时,求直线AB的方程;
(Ⅲ)设切线PA与PB的斜率分别为k1,k2,且k1•k2=
| 1 |
| 2 |
分析:(Ⅰ)利用抛物线的定义即可得出;
(Ⅱ)利用两圆的根轴即可得出;
(Ⅲ)利用直线与圆相切的充要条件、点到直线的距离公式即可得出.
(Ⅱ)利用两圆的根轴即可得出;
(Ⅲ)利用直线与圆相切的充要条件、点到直线的距离公式即可得出.
解答:解:(Ⅰ)由⊙M:x2+y2-8x+12=0,配方得(x-4)2+y2=4,∴圆心M(4,0),半径r=2.
由题意知:4+
=
,解得p=1,
∴抛物线C的方程为y2=2x.
(Ⅱ)设P(2,2),∵P,A,B,M四点共圆,∴此圆的方程为:(x-4)(x-2)+(y-2)(y-0)=0,①
又⊙M:x2-8x+y2+12=0,②
又由①-②得直线AB的方程:x-y-2=0.
(Ⅲ)设过P的直线l方程为y-y0=k(x-x0),由于⊙M与直线l相切,得到
=2,
整理得到:(
-8x0+12)k2+[2y0(4-x0)]k+
-4=0,
∴k1•k2=
=
,即
-12x0+20=0,∴x0=2或10,
经检验得点P坐标为(10,2
).
由题意知:4+
| p |
| 2 |
| 9 |
| 2 |
∴抛物线C的方程为y2=2x.
(Ⅱ)设P(2,2),∵P,A,B,M四点共圆,∴此圆的方程为:(x-4)(x-2)+(y-2)(y-0)=0,①
又⊙M:x2-8x+y2+12=0,②
又由①-②得直线AB的方程:x-y-2=0.
(Ⅲ)设过P的直线l方程为y-y0=k(x-x0),由于⊙M与直线l相切,得到
| |4k+y0-kx0| | ||
|
整理得到:(
| x | 2 0 |
| y | 2 0 |
∴k1•k2=
| ||
|
| 1 |
| 2 |
| x | 2 0 |
经检验得点P坐标为(10,2
| 5 |
点评:熟练掌握抛物线的定义、两圆的根轴的性质、直线与圆相切的充要条件、点到直线的距离公式是解题的关键.

练习册系列答案
相关题目