Question

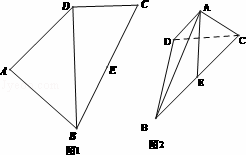
如图，四边形ABCD中（图1），E是BC的中点，DB=2，DC=1，，．将（图1）沿直线BD折起，使二面角A﹣BD﹣C为60°（如图2）

（1）求证：AE⊥平面BDC；

（2）求二面角A﹣DC﹣B的余弦值．

Answer 1

考点：

用空间向量求平面间的夹角；直线与平面垂直的判定；向量语言表述线面的垂直、平行关系；二面角的平面角及求法．

专题：

计算题；证明题．

分析：

（1）先根据条件得到BD⊥平面AEM；进而通过求边长得到AE⊥ME；即可得到结论；

（2）先建立空间直角坐标系，求出两个半平面的法向量的坐标，再代入向量的夹角计算公式即可．

解答：

解：（1）如图取BD中点M，连接AM，ME．

∵．

∴AM⊥BD

∵DB=2，DC=1，⇒DB²+DC²=BC²，

所以△BCD是BC为斜边的直角三角形，BD⊥DC，

∵E是BC的中点，∴ME为△BCD的中位线，

∴ME⊥BD，，

∴∠AME是二面角A﹣BD﹣C的平面角∴∠AME=60°…（3分）

∵AM⊥BD，ME⊥BD且AM、ME是平面AME内两相交于M的直线，

∴BD⊥平面AEM∵AE⊂平面AEM，

∴BD⊥AE

∵，DB=2，

∴△ABD为等腰直角三角形，

∴，，

∴AE²+ME²=1=AM²，

∴AE⊥ME=M，

∴BD∩ME，BD⊂平面BDC，ME⊂面BDC，

∴AE⊥平面BDC…（6分）

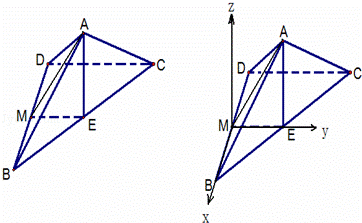
（2）如图，以M为原点MB为x轴，ME为y轴，建立空间直角坐标系M﹣xyz，

则由（1）及已知条件可知B（1，0，0），，，D（﹣1，0，0），C（﹣1，1，0），，…（8分）

设平面ACD的法向量为

则⇒

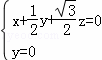
…（10分）

点评：

本题主要考察线面垂直的证明以及二面角的求法．一般在证明线面垂直时，先转化为证明线线垂直．进而得到线面垂直．