Question

已知抛物线y²=2px，直线l经过其焦点且与x轴垂直，并交抛物线于A、B两点，若|AB|=10，P为抛物线的准线上一点，则△ABP的面积为（　　）

A．20

B．25

C．30

D．50

Answer 1

分析：根据抛物线的解析式y²=2px（p＞0），写出抛物线的焦点、对称轴以及准线，然后根据通径|AB|=2p，求出p，△ABP的面积是|AB|与DP乘积一半．

解答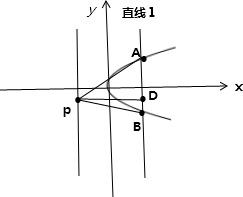：解：由于抛物线的解析式为y²=2px（p＞0），
则焦点为F（

p

2

，0），对称轴为x轴，准线为x=-

p

2

∵直线l经过抛物线的焦点，A、B是l与C的交点，
又∵AB⊥x轴
∴|AB|=2p=10
∴p=5
又∵点P在准线上
∴DP=（

p

2

+|-

p

2

|）=p=5
∴S_△ABP=

1

2

（DP•AB）=

1

2

×5×10=25
故选B．

点评：本题主要考查抛物线焦点、对称轴、准线以及焦点弦的特点；关于直线和圆锥曲线的关系问题一般采取数形结合法．