题目内容
已知等差数列{an}满足a3·a7=-12,a4+a6=-4，求数列{an}的通项公式.
解：∵a4+a6=a3+a7，
∴
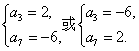
即a3、a7是方程x2+4x-12=0的两根.
∴
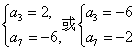
当a3=2，a7=-6时，公差d=
=-2，此时an=a3+(n-3)d=-2n+8；
当a3=-6，a7=2时，d=
，此时an=a3+(n-3)d=2n-16.
练习册系列答案
相关题目
题目内容
已知等差数列{an}满足a3·a7=-12,a4+a6=-4，求数列{an}的通项公式.
解：∵a4+a6=a3+a7，
∴
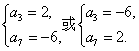
即a3、a7是方程x2+4x-12=0的两根.
∴
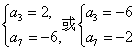
当a3=2，a7=-6时，公差d==-2，此时an=a3+(n-3)d=-2n+8；
当a3=-6，a7=2时，d=，此时an=a3+(n-3)d=2n-16.
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．