题目内容
已知实数x,y满足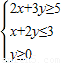 ,则x+3y的最大值是( )
,则x+3y的最大值是( )A.

B.3
C.4
D.

【答案】分析:由实数x,y满足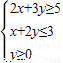 ,作出可行域,由角点法能求出x+3y的最大值.
,作出可行域,由角点法能求出x+3y的最大值.
解答:解:由实数x,y满足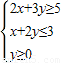 ,
,
作出可行域:
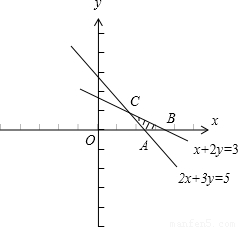
设z=x+3y,
∵A( ,0),∴zA=
,0),∴zA= ;∵B(3,0),∴zB=3;
;∵B(3,0),∴zB=3;
解方程组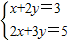 ,得C(1,1),∴zC=1+3=4.
,得C(1,1),∴zC=1+3=4.
∴x+3y的最大值是4.
故选C.
点评:本题考查线性规划问题,难度较小.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.
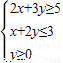 ,作出可行域,由角点法能求出x+3y的最大值.
,作出可行域,由角点法能求出x+3y的最大值.解答:解:由实数x,y满足
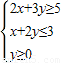 ,
,作出可行域:

设z=x+3y,
∵A(
 ,0),∴zA=
,0),∴zA= ;∵B(3,0),∴zB=3;
;∵B(3,0),∴zB=3;解方程组
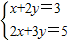 ,得C(1,1),∴zC=1+3=4.
,得C(1,1),∴zC=1+3=4.∴x+3y的最大值是4.
故选C.
点评:本题考查线性规划问题,难度较小.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目