题目内容
设数列{an}的前n项和为Sn,满足 ,且a1,a2+5,a3成等差数列.
,且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 .
.
解:(1)在2Sn=an+1-2n+1+1中,
令n=1得:2S1=a2-22+1,
令n=2得:2S2=a3-23+1,
解得:a2=2a1+3,a3=6a1+13
又2(a2+5)=a1+a3
解得a1=1
(2)由2Sn=an+1-2n+1+1,
 得an+2=3an+1+2n+1,
得an+2=3an+1+2n+1,
又a1=1,a2=5也满足a2=3a1+21,
所以an+1=3an+2n对n∈N*成立
∴an+1+2n+1=3(an+2n),又a1=1,a1+21=3,
∴an+2n=3n,
∴an=3n-2n;
(3)(法一)
∵an=3n-2n=(3-2)(3n-1+3n-2×2+3n-3×22+…+2n-1)≥3n-1
∴ ≤
≤ ,
,
∴ +
+ +
+ +…+
+…+ ≤1+
≤1+ +
+ +…+
+…+ =
= <
< ;
;
(法二)∵an+1=3n+1-2n+1>2×3n-2n+1=2an,
∴ <
< •
• ,,
,,
当n≥2时, <
< •
• ,
,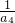 <
< •
• ,
, ,
,
… <
< •
• ,
,
累乘得: <
< •
• ,
,
∴ +
+ +
+ +…+
+…+ ≤1+
≤1+ +
+ ×
× +…+
+…+ ×
× <
< <
< .
.
分析:(1)在2Sn=an+1-2n+1+1中,令分别令n=1,2,可求得a2=2a1+3,a3=6a1+13,又a1,a2+5,a3成等差数列,从而可求得a1;
(2)由2Sn=an+1-2n+1+1, 得an+2=3an+1+2n+1①,an+1=3an+2n②,由①②可知{an+2n}为首项是3,3为公比的等比数列,从而可求an;
得an+2=3an+1+2n+1①,an+1=3an+2n②,由①②可知{an+2n}为首项是3,3为公比的等比数列,从而可求an;
(3)(法一),由an=3n-2n=(3-2)(3n-1+3n-2×2+3n-3×22+…+2n-1)≥3n-1可得 ≤
≤ ,累加后利用等比数列的求和公式可证得结论;
,累加后利用等比数列的求和公式可证得结论;
(法二)由an+1=3n+1-2n+1>2×3n-2n+1=2an可得, <
< •
• ,于是当n≥2时,
,于是当n≥2时, <
< •
• ,
,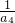 <
< •
• ,
, ,…,
,…, <
< •
• ,累乘得:
,累乘得: <
< •
• ,从而可证得
,从而可证得 +
+ +
+ +…+
+…+ <
< .
.
点评:本题考查数列与不等式的综合,考查数列递推式,着重考查等比数列的求和,着重考查放缩法的应用,综合性强,运算量大,属于难题.
令n=1得:2S1=a2-22+1,
令n=2得:2S2=a3-23+1,
解得:a2=2a1+3,a3=6a1+13
又2(a2+5)=a1+a3
解得a1=1
(2)由2Sn=an+1-2n+1+1,
 得an+2=3an+1+2n+1,
得an+2=3an+1+2n+1,又a1=1,a2=5也满足a2=3a1+21,
所以an+1=3an+2n对n∈N*成立
∴an+1+2n+1=3(an+2n),又a1=1,a1+21=3,
∴an+2n=3n,
∴an=3n-2n;
(3)(法一)
∵an=3n-2n=(3-2)(3n-1+3n-2×2+3n-3×22+…+2n-1)≥3n-1
∴
 ≤
≤ ,
,∴
 +
+ +
+ +…+
+…+ ≤1+
≤1+ +
+ +…+
+…+ =
= <
< ;
;(法二)∵an+1=3n+1-2n+1>2×3n-2n+1=2an,
∴
 <
< •
• ,,
,,当n≥2时,
 <
< •
• ,
,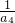 <
< •
• ,
, ,
,…
 <
< •
• ,
,累乘得:
 <
< •
• ,
,∴
 +
+ +
+ +…+
+…+ ≤1+
≤1+ +
+ ×
× +…+
+…+ ×
× <
< <
< .
.分析:(1)在2Sn=an+1-2n+1+1中,令分别令n=1,2,可求得a2=2a1+3,a3=6a1+13,又a1,a2+5,a3成等差数列,从而可求得a1;
(2)由2Sn=an+1-2n+1+1,
 得an+2=3an+1+2n+1①,an+1=3an+2n②,由①②可知{an+2n}为首项是3,3为公比的等比数列,从而可求an;
得an+2=3an+1+2n+1①,an+1=3an+2n②,由①②可知{an+2n}为首项是3,3为公比的等比数列,从而可求an;(3)(法一),由an=3n-2n=(3-2)(3n-1+3n-2×2+3n-3×22+…+2n-1)≥3n-1可得
 ≤
≤ ,累加后利用等比数列的求和公式可证得结论;
,累加后利用等比数列的求和公式可证得结论;(法二)由an+1=3n+1-2n+1>2×3n-2n+1=2an可得,
 <
< •
• ,于是当n≥2时,
,于是当n≥2时, <
< •
• ,
,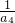 <
< •
• ,
, ,…,
,…, <
< •
• ,累乘得:
,累乘得: <
< •
• ,从而可证得
,从而可证得 +
+ +
+ +…+
+…+ <
< .
.点评:本题考查数列与不等式的综合,考查数列递推式,着重考查等比数列的求和,着重考查放缩法的应用,综合性强,运算量大,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目