题目内容
21.已知f(x)=ax3+bx2+cx在区间[0,1]上是增函数,在区间(-(Ⅰ)求f(x)的解析式;
(Ⅱ)若在区间[0,m](m>0)上恒有f(x) ≤x成立,求m的取值范围.
解:(Ⅰ)![]() (x)=3ax2+2bx+c,由已知
(x)=3ax2+2bx+c,由已知![]() (0)=
(0)=![]() (1)=0,
(1)=0,
即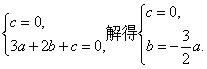
∴![]() (x)=3ax2-3ax. ∴
(x)=3ax2-3ax. ∴![]()
![]() ∴a=-2. ∴f(x)=-2x3+3x2.
∴a=-2. ∴f(x)=-2x3+3x2.
(Ⅱ)令f(x) ≤x,即-2x3+3x2-x≤0,
∴x(2x-1)(x-1) ≥0, ∴0≤x≤![]() 或x≥1.
或x≥1.
又f(x) ≤x在区间[0,m]上的恒成立, ∴0<m≤![]() .
.

练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |