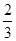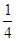题目内容
记 分别是投掷两次骰子所得的数字,则方程
分别是投掷两次骰子所得的数字,则方程 有两个不同实根的概率为( )
有两个不同实根的概率为( )
A.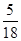 | B. | C. | D. |
B
解析试题分析:记 分别是投掷两次骰子所得的数字,其结果共有
分别是投掷两次骰子所得的数字,其结果共有 ,
,
共36种情况,要满足 有两个不同实根,需∆=
有两个不同实根,需∆= ,满足此条件的基本事件有(3,1),(4,1),(5,1),(5,2),(5,3),(6,1),(6,2),(6,3),(6,4),共9个,所以其概率为
,满足此条件的基本事件有(3,1),(4,1),(5,1),(5,2),(5,3),(6,1),(6,2),(6,3),(6,4),共9个,所以其概率为 。
。
考点:古典概型。
点评:计算古典概型所包含基本事件总数的方法:(1)树形图;(2)列表法;(3)也可以用坐标系中的点表示;(4)用排列、组合求基本事件的总数。

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
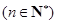 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
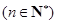 的判断正确的是
的判断正确的是
A. 有最小值,且最小值为 有最小值,且最小值为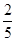 | B. 有最大值,且最大值为 有最大值,且最大值为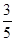 |
C. 有最小值,且最小值为 有最小值,且最小值为 | D. 有最大值,且最大值为 有最大值,且最大值为 |
已知关于 的方程
的方程 ,若
,若 ,记“该方程有实数根
,记“该方程有实数根 且满足
且满足 ” 为事件A,则事件A发生的概率为( )
” 为事件A,则事件A发生的概率为( )
A. | B. | C. | D. |
一个均匀正方体玩具的各个面上分别标有数字1,2,3,4,5,6.将这个玩具向上抛掷1次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过3,事件C表示向上的一面出现的点数不小于4,则( )
| A.A与B是互斥而非对立事件 | B.A与B是对立事件 |
| C.B与C是互斥而非对立事件 | D.B与C是对立事件 |


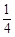


 ,则方差
,则方差 ( )
( ) B.
B. C.
C. D.
D.
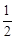
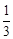
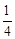
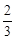
 ,则
,则 的概率为:( )
的概率为:( )