题目内容
已知函数f(x)=asin(2 +b(x∈R,a<0,ω>0)的最小正周期为π,函数f(x)的最大值是
+b(x∈R,a<0,ω>0)的最小正周期为π,函数f(x)的最大值是 ,最小值是
,最小值是 .
.
(1)求ω,a,b的值;
(2)求出f(x)的单调递增区间;
(3)指出当f(x)取得最大值和最小值时x的集合.
解:(1)∵最小正周期为π,由周期公式可得,2ω=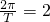 ,∴ω=1
,∴ω=1
∵函数f(x)的最大值是 ,最小值是
,最小值是 ,a<0
,a<0
 ∴
∴
∴
(2)(x)= sin(2x+
sin(2x+
由 可得
可得
∴函数的单调增区间为:
(3)f(x)最大值时,2x+ ,此时有
,此时有 ;
;
f(x)最小值时, ,此时有
,此时有
分析:(1)由周期为π,根据周期公式可得,2ω=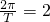 ,则ω=1由函数f(x)的最大值是
,则ω=1由函数f(x)的最大值是 ,最小值是
,最小值是 ,a<0,可得
,a<0,可得 解得答案;
解得答案;
(2)要求函数(x)= sin(2x+
sin(2x+ 的单调增区间,可求f(x)=
的单调增区间,可求f(x)= sin(2x+
sin(2x+ 的单调减区间,由
的单调减区间,由 可得函数的单调增区间;
可得函数的单调增区间;
(3)f(x)最大值时,2x+ ;f(x)最小值时,
;f(x)最小值时, ,求解即可.
,求解即可.
点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定函数的解析式,考查了正弦函数的单调区间及函数的最值的求解及最值取得的条件,考查了对基础知识的综合运用能力.
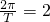 ,∴ω=1
,∴ω=1∵函数f(x)的最大值是
 ,最小值是
,最小值是 ,a<0
,a<0 ∴
∴
∴

(2)(x)=
 sin(2x+
sin(2x+
由
 可得
可得
∴函数的单调增区间为:

(3)f(x)最大值时,2x+
 ,此时有
,此时有 ;
;f(x)最小值时,
 ,此时有
,此时有
分析:(1)由周期为π,根据周期公式可得,2ω=
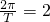 ,则ω=1由函数f(x)的最大值是
,则ω=1由函数f(x)的最大值是 ,最小值是
,最小值是 ,a<0,可得
,a<0,可得 解得答案;
解得答案;(2)要求函数(x)=
 sin(2x+
sin(2x+ 的单调增区间,可求f(x)=
的单调增区间,可求f(x)= sin(2x+
sin(2x+ 的单调减区间,由
的单调减区间,由 可得函数的单调增区间;
可得函数的单调增区间;(3)f(x)最大值时,2x+
 ;f(x)最小值时,
;f(x)最小值时, ,求解即可.
,求解即可.点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定函数的解析式,考查了正弦函数的单调区间及函数的最值的求解及最值取得的条件,考查了对基础知识的综合运用能力.

练习册系列答案
相关题目