题目内容
已知a＞0且a≠1，f（x）=x2-ax，当x∈（-1，1）时均有f（x）＜
，则实数a的取值范围是（ ）A．
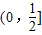∪[2，+∞）B．
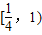∪（1，4]C．
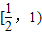∪（1，2]D．
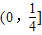∪[4，+∞）
【答案】分析：由题意可知，ax＞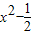
在（-1，1）上恒成立，令y1=ax，y2=
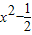，结合图象，列出不等式组，解不等式组，求出a的取值范围．
解答：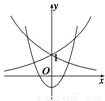
解：由题意可知，ax＞
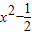在（-1，1）上恒成立，令y1=ax，y2=
，
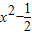由图象知：0＜a＜1时a1≥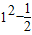
=
，即
≤a＜1；
当a＞1时，a-1≥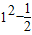
=
，可得
1＜a≤2．
∴
≤a＜1或1＜a≤2．
故选 C．
点评：本题考查不等式组的解法，体现了数形结合和转化的数学思想．
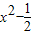在（-1，1）上恒成立，令y1=ax，y2=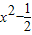，结合图象，列出不等式组，解不等式组，求出a的取值范围．解答：
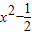解：由题意可知，ax＞ 在（-1，1）上恒成立，令y1=ax，y2=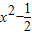，由图象知：0＜a＜1时a1≥
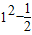=，即≤a＜1；当a＞1时，a-1≥
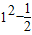=，可得1＜a≤2．
∴
≤a＜1或1＜a≤2．故选 C．
点评：本题考查不等式组的解法，体现了数形结合和转化的数学思想．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目