题目内容
已知AB是⊙O的直径,PA垂直于⊙O所在平面,C是⊙O上一点,且∠CAB=60°,PA=a,AB=2a.
求:(1)三棱锥P—ABC的侧面积;
(2)三棱锥P—OBC的体积.
答案:
解析:
解析:
| 解:由于这个三棱锥不是正三棱锥,故要求其侧面积需分别求出各个侧面的面积.
(1)∵AB是⊙O的直径,∴BC⊥CA. ∵PA⊥⊙O所在平面,∴PA⊥BC. ∴BC⊥面PAC.∴BC⊥PC,即△PBC是Rt△. 在Rt△ABC中,∠CAB=60°,AB=2a,∴AC=a,BC= 在Rt△APC中,AC=a,PA=a,∴PC= ∴S△APC= ∴三棱锥P—ABC的侧面积为 (2)由于△OBC与△OAC面积相等,因此S△OBC= ∴三棱锥P—OBC的体积为V=
|

练习册系列答案
相关题目
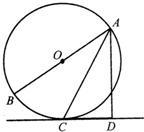 如图,已知AB是⊙O的直径,AC为弦,且平分∠BAD,AD⊥CD,垂足为D.
如图,已知AB是⊙O的直径,AC为弦,且平分∠BAD,AD⊥CD,垂足为D. 如图,已知AB是⊙O的直径,AC是弦,AD⊥CE,垂足为D,AC平分∠BAD.
如图,已知AB是⊙O的直径,AC是弦,AD⊥CE,垂足为D,AC平分∠BAD. 如图,已知AB是⊙O的直径,AB⊥CD于E,切线BF交AD的延长线于F,若AB=10,CD=8,则切线BF的长是
如图,已知AB是⊙O的直径,AB⊥CD于E,切线BF交AD的延长线于F,若AB=10,CD=8,则切线BF的长是 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点. 如图,已知AB是⊙O的直径,⊙O的切线PA与弦BC的延长线相交于点P,∠PBA的平分线交PA于点D,∠ABC=30°.
如图,已知AB是⊙O的直径,⊙O的切线PA与弦BC的延长线相交于点P,∠PBA的平分线交PA于点D,∠ABC=30°.