题目内容
【题目】已知椭圆E:![]() (
(![]() )的左右焦点分别是
)的左右焦点分别是![]()
![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆E上.
在椭圆E上.
(1)求椭圆E的方程;
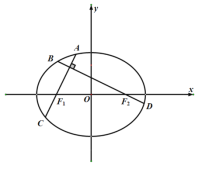
(2)如图,分别过![]()
![]() 作两条互相垂直的弦AC与BD,求
作两条互相垂直的弦AC与BD,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由离心率求出![]() 关系,化简标准方程,将点
关系,化简标准方程,将点![]() 代入方程,即可求解;
代入方程,即可求解;
(2)先考率两直线斜率为0或斜率不存在的情况,当两直线斜率存在且不等于0,设出直线方程,可以是点斜式(或![]() 轴截距式),与椭圆方程联立,求出相交弦长,进而得到
轴截距式),与椭圆方程联立,求出相交弦长,进而得到![]() 关于斜率(或斜率倒数)的目标函数,转化求函数的最值,即可求解.
关于斜率(或斜率倒数)的目标函数,转化求函数的最值,即可求解.
解:(1)由已知![]() ,
,![]() ,
,
![]()
![]()
将点![]() 代入得
代入得![]() ,
,
![]() ,
,![]()
![]() 椭圆E方程为:
椭圆E方程为:![]() .
.
(2)解法一:由已知![]() ,
,
①当![]() 轴或在
轴或在![]() 轴上时,
轴上时,
![]() ,
,![]() ,或
,或![]() ,
,![]() ,
,
![]()
②当直线斜率存在且不为0时,
![]() ,
,![]() 设直线AC方程为:
设直线AC方程为:![]()
联立![]() 得:
得:![]()
设![]() ,
,![]()
则![]() ,
,![]()
![]()
![]() ,由椭圆对称性,以
,由椭圆对称性,以![]() 代换上式中的k得:
代换上式中的k得:
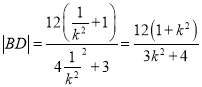 ,
,
思路一: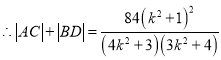
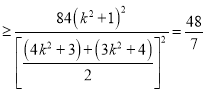 ,
,
当且仅当![]() 即
即![]() 时,取“=”
时,取“=”
而![]() ,
,![]() 有最小值
有最小值![]()
思路二:设![]() ,则
,则![]() ,
,![]()
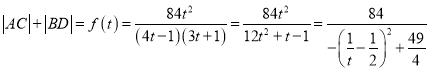
当且仅当![]() ,
,![]() ,
,![]()
即![]() 时,有最小值
时,有最小值![]() .
.
而![]() ,
,![]() 有最小值
有最小值![]()
解法二:由已知![]() ,设直线AC:
,设直线AC:![]()
联立![]() 得:
得:![]()
设![]() ,
,![]() 则
则![]() ,
,![]()
![]()
![]() ,由椭圆对称性,以
,由椭圆对称性,以![]() 代换上式中的
代换上式中的![]() 得:
得:
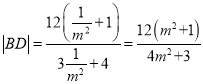 .
.
思路一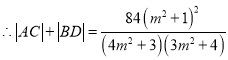
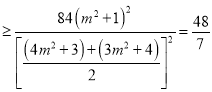 ,
,
当且仅当![]() 即
即![]() 时,取“=”,
时,取“=”,
![]() 有最小值
有最小值![]() .
.
思路二:设![]() 则
则![]()
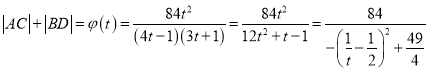
当且仅当![]() ,
,![]() 即
即![]() 时,有最小值
时,有最小值![]() .
.
![]() 有最小值
有最小值![]() .
.

 互动课堂系列答案
互动课堂系列答案【题目】2017年3月18日,国务院办公厅发布了《生活垃圾分类制度实施方案》,我市环保部门组织了一次垃圾分类知识的网络问卷调查,每位市民都可以通过电脑网络或手机微信平台参与,但仅有一次参加机会工作人员通过随机抽样,得到参与网络问卷调查的100人的得分(满分按100分计)数据,统计结果如下表.
组别 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
(1)环保部门规定:问卷得分不低于70分的市民被称为“环保关注者”.请列出![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下,认为是否为“环保关注者”与性别有关?
的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.现在从本次调查的“环保达人”中利用分层抽样的方法随机抽取5名市民参与环保知识问答,再从这5名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“环保达人”又有女“环保达人”的概率.
附表及公式: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|