题目内容
已知M={(x,y)|y2=2x},N={(x,y)|(x-a)2+y2=9},求M∩N≠
解析:考虑M∩N≠![]() 的充要条件是方程组?
的充要条件是方程组?
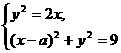 至少有一组实数解.?
至少有一组实数解.?
即x2+2(1-a)x+a2-9=0至少有一个非负根
由Δ≥0.得a≤5.在此前提下
又∵上述方程有两种负根的充要条件是:?
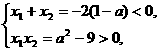 即a<-3.
即a<-3.
于是这个方程至少有一非负根的a的取值范围是-3≤a≤5,此即为所求的充要条件.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
题目内容
已知M={(x,y)|y2=2x},N={(x,y)|(x-a)2+y2=9},求M∩N≠
解析:考虑M∩N≠![]() 的充要条件是方程组?
的充要条件是方程组?
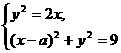 至少有一组实数解.?
至少有一组实数解.?
即x2+2(1-a)x+a2-9=0至少有一个非负根
由Δ≥0.得a≤5.在此前提下
又∵上述方程有两种负根的充要条件是:?
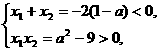 即a<-3.
即a<-3.
于是这个方程至少有一非负根的a的取值范围是-3≤a≤5,此即为所求的充要条件.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案