题目内容
x+1).
(1)求f(0),f(1);
(2)求函数f(x)的解析式;
(3)若f(a-1)<-1,求实数a的取值范围.
解析: (1)因为当x≤0时,f(x)= (-x+1),
(-x+1),
所以f(0)=0.
又函数f(x)是定义在R上的偶函数,所以f(1)=f(-1)= [-(-1)+1]=
[-(-1)+1]= 2=-1,即f(1)=-1.
2=-1,即f(1)=-1.
(2)令x>0,则-x<0,
从而f(-x)= (x+1)=f(x),
(x+1)=f(x),
∴x>0时,f(x)= (x+1).
(x+1).
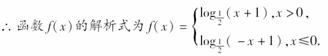
(3)设x1,x2是任意两个值,且x1<x2≤0,
则-x1>-x2≥0,
∴1-x1>1-x2>0.
∵f(x2)-f(x1)= (-x2+1)-
(-x2+1)- (-x1+1)=
(-x1+1)=
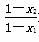 >
> 1=0,
1=0,
∴f(x2)>f(x1),
∴f(x)= (-x+1)在(-∞,0]上为增函数.
(-x+1)在(-∞,0]上为增函数.
又f(x)是定义在R上的偶函数,
∴f(x)在(0,+∞)上为减函数.
∵f(a-1)<-1=f(1),∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞,0)∪(2,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
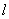 与双曲线
与双曲线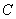 交于
交于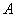 ,
,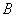 两点(
两点(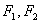 为双曲线的两个焦点,则
为双曲线的两个焦点,则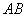 的垂直平分线上
的垂直平分线上  =_____________________________.
=_____________________________. =3
=3 ,点O在线段CD上(与点C、D不重合),若
,点O在线段CD上(与点C、D不重合),若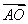 =x
=x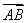 +(1-x)
+(1-x)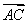 ,则x的取值范围是( )
,则x的取值范围是( )
 -1 B.
-1 B.