题目内容
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+ 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集.
)(x+4)≤0的解集.
(1)求A∩B;
(2)若C⊆∁RA,求a的取值范围.
【答案】
(1) (-4,-3]∪[1,2) (2) 
【解析】本题主要考查了集合的交并补混合运算,较为简单,关键是将各集合的元素计算出来.
(1)分别计算出几何A,B,再计算A∩B即可;
(2)根据条件再由(1)容易计算.
解:(1)由-x2-2x+8>0,解得A=(-4,2),
又y=x+ =(x+1)+
=(x+1)+ -1,
-1,
所以B=(-∞,-3]∪ [1,+∞).
所以A∩B=(-4,-3]∪[1,2).
(2)因为∁RA=(-∞,-4]∪[2,+∞).
由 (x+4)≤0,知a≠0.
(x+4)≤0,知a≠0.
①当a>0时,由 (x+4)≤0,得C=
(x+4)≤0,得C= ,不满足C⊆∁RA;
,不满足C⊆∁RA;
②当a<0时,由 (x+4)≥0,得C=(-∞,-4)∪
(x+4)≥0,得C=(-∞,-4)∪ ,欲使C⊆∁RA,则
,欲使C⊆∁RA,则 ≥2,
≥2,
解得- ≤a<0或0<a≤
≤a<0或0<a≤ .
.
又a<0,所以- ≤a<0.
≤a<0.
综上所述,所求a的取值范围是  .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax-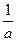 )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围. 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.