题目内容
已知函数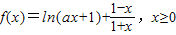 ,其中a>0.
,其中a>0.(1)若f(x)在x=1处取得极值,求a的值;
(2)求f(x)的单调区间;
(3)若f(x)的最小值为1,求a的取值范围.
【答案】分析:(1)对函数求导,令f′(1)=0,即可解出a值.
(2)f′(x)>0,对a的取值范围进行讨论,分类解出单调区间.a≥2时,在区间(0,+∞)上是增函数,
(3)由(2)的结论根据单调性确定出最小值,当a≥2时,由(II)知,f(x)的最小值为f(0)=1,恒成立;当0<a<2时,判断知最小值小于1,此时a无解.当0<a<2时,(x)的单调减区间为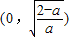 ,单调增区间为
,单调增区间为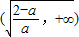
解答:解:(1)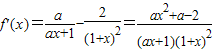 ,
,
∵f′(x)在x=1处取得极值,f′(1)=0
即 a+a-2=0,解得 a=1
(2)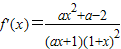 ,
,
∵x≥0,a>0,
∴ax+1>0
①当a≥2时,在区间(0,+∞)上f′(x)>0.
∴f(x)的单调增区间为(0,+∞)
②当0<a<2时,由f′(x)>0解得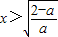
由
∴f(x)的单调减区间为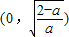 ,单调增区间为
,单调增区间为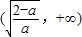
(3)当a≥2时,由(II)知,f(x)的最小值为f(0)=1
当0<a<2时,由(II)②知,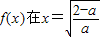 处取得最小值
处取得最小值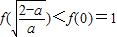 ,
,
综上可知,若f(x)的最小值为1,则a的取值范围是[2,+∞)
点评:考查导数法求单调区间与求最值,本类题型是导数的主要运用.
(2)f′(x)>0,对a的取值范围进行讨论,分类解出单调区间.a≥2时,在区间(0,+∞)上是增函数,
(3)由(2)的结论根据单调性确定出最小值,当a≥2时,由(II)知,f(x)的最小值为f(0)=1,恒成立;当0<a<2时,判断知最小值小于1,此时a无解.当0<a<2时,(x)的单调减区间为
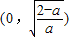 ,单调增区间为
,单调增区间为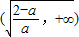
解答:解:(1)
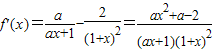 ,
,∵f′(x)在x=1处取得极值,f′(1)=0
即 a+a-2=0,解得 a=1
(2)
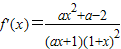 ,
,∵x≥0,a>0,
∴ax+1>0
①当a≥2时,在区间(0,+∞)上f′(x)>0.
∴f(x)的单调增区间为(0,+∞)
②当0<a<2时,由f′(x)>0解得
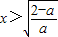
由

∴f(x)的单调减区间为
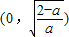 ,单调增区间为
,单调增区间为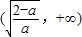
(3)当a≥2时,由(II)知,f(x)的最小值为f(0)=1
当0<a<2时,由(II)②知,
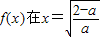 处取得最小值
处取得最小值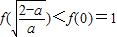 ,
,综上可知,若f(x)的最小值为1,则a的取值范围是[2,+∞)
点评:考查导数法求单调区间与求最值,本类题型是导数的主要运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.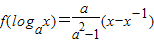 ,其中a>0且a≠1.
,其中a>0且a≠1.