题目内容
函数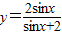 的值域为 .
的值域为 .
【答案】分析:利用分类变量法或利用三角函数的有界性求值域.
解答:解:方法1:分类变量法
因为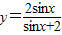 =
=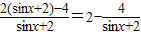 ,
,
因为-1≤sinx≤1,所以1≤sinx+2≤3,
所以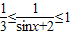 ,
,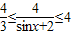 ,
,
所以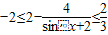 ,即函数的值域为
,即函数的值域为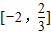 .
.
方法2:函数的性质法.
因为-1≤sinx≤1,所以y(sinx+2)=2sinx,
即(2-y)sinx=2y,
若y=2,则0=4不成立,所以y≠2.
所以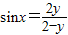 ,
,
因为-1≤sinx≤1,所以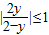 ,
,
解得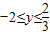 ,即函数的值域为
,即函数的值域为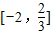 .
.
点评:本题主要考查了函数的值域求法,利用三角函数的有界性是解决本题的关键,要求熟练掌握求函数值域的几种常见方法.
解答:解:方法1:分类变量法
因为
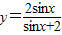 =
=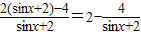 ,
,因为-1≤sinx≤1,所以1≤sinx+2≤3,
所以
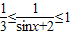 ,
,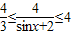 ,
,所以
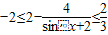 ,即函数的值域为
,即函数的值域为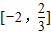 .
.方法2:函数的性质法.
因为-1≤sinx≤1,所以y(sinx+2)=2sinx,
即(2-y)sinx=2y,
若y=2,则0=4不成立,所以y≠2.
所以
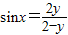 ,
,因为-1≤sinx≤1,所以
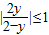 ,
,解得
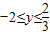 ,即函数的值域为
,即函数的值域为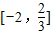 .
.点评:本题主要考查了函数的值域求法,利用三角函数的有界性是解决本题的关键,要求熟练掌握求函数值域的几种常见方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: