题目内容
已知函数f(x)的定义域为[0,1],且同时满足:①对于任意x∈[0,1],总有f(x)≥3;②f(1)=4;③若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(I)求f(0)的值;
(II)求函数f(x)的最大值;
(III)设数列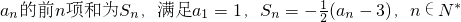 ,求证:
,求证: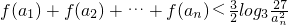 .
.
(Ⅰ) 解:令x1=x2=0,则有f(0)≥2f(0)-3,即f(0)≤3
又对于任意x∈[0,1],总有f(x)≥3,
∴f(0)=3 (3分)
(Ⅱ)解:任取x1,x2∈[0,1],x1<x2,
f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-3
∵0≤x1<x2≤1,则0<x2-x1<1,
∴f(x2-x1)≥3
∴f(x2)≥f(x1)+3-3=f(x1),即f(x)在[0,1]上递增.
∴当x∈[0,1]时,f(x)≤f(1)=4
∴f(x)的最大值为4 (6分)
(Ⅲ)证明:当n>1时,an=Sn-Sn-1=- (an-3)-
(an-3)- (an-1-3),
(an-1-3),
∴
∴数列{an}是以a1=1为首项,公比为 的等比数列.
的等比数列.
∴an= (8分)
(8分)
f(1)=f[3n-1 ]=f[
]=f[ +(3n-1-1)×
+(3n-1-1)× ]≥f(
]≥f( )+f[(3n-1-1)×
)+f[(3n-1-1)× ]-3≥…
]-3≥…
即 4≥3n-1f( )-3n+3.(10分)
)-3n+3.(10分)
∴f( )≤
)≤ ,即f(an)≤3+
,即f(an)≤3+ .
.
∴f(a1)+f(a2)+…+f(an)≤(3+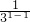 )+(3+
)+(3+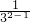 )+…+(3+
)+…+(3+ )
)
=3n+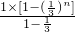 =3n+
=3n+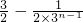 <3n+
<3n+ =3(n+
=3(n+ ).
).
又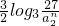 =
= log333•32n-2=
log333•32n-2= (2n+1)=3(n+
(2n+1)=3(n+ ),
),
∴原不等式成立.(14分)
分析:(Ⅰ)直接取x1=0,x2=0利用f(x1+x2)≥f(x1)+f(x2)-3可得:f(0)≤3,再结合已知条件f(0)≥3即可求得f(0)=3;
(Ⅱ)由0≤x1<x2≤1,则0<x2-x1<1,故有f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-3>f(x1),即f(x)在[0,1]内是增函数,故函数f(x)的最大值为f(1);
(Ⅲ)先证明数列{an}是以a1=1为首项,公比为 的等比数列,进而可得f(1)=f[3n-1
的等比数列,进而可得f(1)=f[3n-1 ]=f[
]=f[ +(3n-1-1)×
+(3n-1-1)× ]≥f(
]≥f( )+f[(3n-1-1)×
)+f[(3n-1-1)× ]-3≥…,即 4≥3n-1f(
]-3≥…,即 4≥3n-1f( )-3n+3,即f(an)≤3+
)-3n+3,即f(an)≤3+ ,从而可证不等式.
,从而可证不等式.
点评:本题主要是在新定义下对抽象函数进行考查,在做关于新定义的题目时,一定要先研究定义,在理解定义的基础上再做题.解题时要认真审题,合理运用条件.
又对于任意x∈[0,1],总有f(x)≥3,
∴f(0)=3 (3分)
(Ⅱ)解:任取x1,x2∈[0,1],x1<x2,
f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-3
∵0≤x1<x2≤1,则0<x2-x1<1,
∴f(x2-x1)≥3
∴f(x2)≥f(x1)+3-3=f(x1),即f(x)在[0,1]上递增.
∴当x∈[0,1]时,f(x)≤f(1)=4
∴f(x)的最大值为4 (6分)
(Ⅲ)证明:当n>1时,an=Sn-Sn-1=-
 (an-3)-
(an-3)- (an-1-3),
(an-1-3),∴

∴数列{an}是以a1=1为首项,公比为
 的等比数列.
的等比数列.∴an=
 (8分)
(8分)f(1)=f[3n-1
 ]=f[
]=f[ +(3n-1-1)×
+(3n-1-1)× ]≥f(
]≥f( )+f[(3n-1-1)×
)+f[(3n-1-1)× ]-3≥…
]-3≥…即 4≥3n-1f(
 )-3n+3.(10分)
)-3n+3.(10分)∴f(
 )≤
)≤ ,即f(an)≤3+
,即f(an)≤3+ .
.∴f(a1)+f(a2)+…+f(an)≤(3+
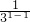 )+(3+
)+(3+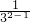 )+…+(3+
)+…+(3+ )
)=3n+
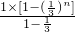 =3n+
=3n+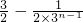 <3n+
<3n+ =3(n+
=3(n+ ).
).又
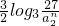 =
= log333•32n-2=
log333•32n-2= (2n+1)=3(n+
(2n+1)=3(n+ ),
),∴原不等式成立.(14分)
分析:(Ⅰ)直接取x1=0,x2=0利用f(x1+x2)≥f(x1)+f(x2)-3可得:f(0)≤3,再结合已知条件f(0)≥3即可求得f(0)=3;
(Ⅱ)由0≤x1<x2≤1,则0<x2-x1<1,故有f(x2)=f[(x2-x1)+x1]≥f(x2-x1)+f(x1)-3>f(x1),即f(x)在[0,1]内是增函数,故函数f(x)的最大值为f(1);
(Ⅲ)先证明数列{an}是以a1=1为首项,公比为
 的等比数列,进而可得f(1)=f[3n-1
的等比数列,进而可得f(1)=f[3n-1 ]=f[
]=f[ +(3n-1-1)×
+(3n-1-1)× ]≥f(
]≥f( )+f[(3n-1-1)×
)+f[(3n-1-1)× ]-3≥…,即 4≥3n-1f(
]-3≥…,即 4≥3n-1f( )-3n+3,即f(an)≤3+
)-3n+3,即f(an)≤3+ ,从而可证不等式.
,从而可证不等式.点评:本题主要是在新定义下对抽象函数进行考查,在做关于新定义的题目时,一定要先研究定义,在理解定义的基础上再做题.解题时要认真审题,合理运用条件.

练习册系列答案
相关题目
