题目内容
等差数列{an}的前n项和分别为Sn=An2+n,且S2=6;函数y=g(x)是函数f(x)=2x的反函数,且cn=g(cn-1)(n∈N,n>1),c1=1.(1)求常数A的值及函数y=g(x)的解析式;
(2)求数列{an}及{cn}的通项公式;
(3)若dn=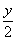 ,试求d1+d2+…+dn.
,试求d1+d2+…+dn.
解:(1)由S2=6知:4A+2=6 解得A=1
令y=2x 得x=![]() ,即g(x)=
,即g(x)= ![]()
(2)当n=1时,a1=Sl=2,
当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n
综合之:an=2n
由题意得:cn=![]() cn-1
cn-1
∴数列{cn}是![]() 为公比,以c1=1为首项的等比数列.
为公比,以c1=1为首项的等比数列.
∴cn=(![]() )n-1
)n-1
(3)当n=2k+1时,d1+d2+…+dn
=(a1+a3+…+a2k+1)+(c2+c4+…+c2k)
=2(k+1)2+![]() [1-(
[1-(![]() )k]
)k]
=2(![]() )2+
)2+![]() [1-
[1-![]() ]
]
当n=2k时,d1+d2+…+dn
=(a1+a3+…+a2k-1)+(c2+c4+…+c2k)
=(2k+1)k+![]() [1-(
[1-(![]() )k]
)k]
=![]()
综合之:d1+d2+…+dn
=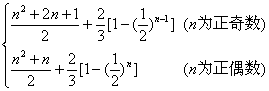

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |