题目内容
已知函数 ,在
,在 处连续.
处连续.
(1)求函数 的单调减区间;
的单调减区间;
(2)若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
解:(1)由 在
在 处连续,可得
处连续,可得 ,故
,故 ………………1分
………………1分
∴ …………………………2分
…………………………2分
当 时,
时, ,令
,令 ,可得
,可得 ……………………4分
……………………4分
当 时,
时, ,故
,故 ………………5分
………………5分
所以函数 的单调减区间为(0,
的单调减区间为(0, )………………6分
)………………6分
(2)设
当 时,
时, ,
,
令 ,可得
,可得 或
或 ,即
,即 ;
;
令 ,可得
,可得
可得 为函数
为函数 的单调增区间,
的单调增区间, 为函数
为函数 的单调减区间.
的单调减区间.
当 时,
时, ,
,
故当 时,
时, .
.
可得 为函数
为函数 的单调减区间.
的单调减区间.
又函数 在
在 处连续,
处连续,
于是函数 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 ………………10分
………………10分
所以函数 的最大值为
的最大值为 ,要使不等式
,要使不等式 对一切
对一切 恒成立,
恒成立,
即 对一切
对一切 恒成立,
恒成立,
又 ,
,
故 的取值范围为
的取值范围为 …………………………12分
…………………………12分

练习册系列答案
相关题目
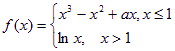 ,在x=1处连续.
,在x=1处连续. ,在x=1处连续,则实数a的值为 .
,在x=1处连续,则实数a的值为 . ,在x=1处连续,则实数a的值为 .
,在x=1处连续,则实数a的值为 . ,在x=1处连续,则实数a的值为 .
,在x=1处连续,则实数a的值为 .