题目内容
在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、BC的中点,M为棱AA1上的点.
(1)证明:A1B1⊥C1D;
(2)当AM= 时,求二面角M﹣DE﹣A的大小.
时,求二面角M﹣DE﹣A的大小.
(1)证明:A1B1⊥C1D;
(2)当AM=
 时,求二面角M﹣DE﹣A的大小.
时,求二面角M﹣DE﹣A的大小.
(1)证明:以C为坐标原点建立空间直角坐标系C﹣xyz,则
A1(1,0,1),B1(0,1,1),C1(0,0,1),D( ,
, ,0),
,0),
 =(﹣1,1,0),
=(﹣1,1,0), =(
=( ,
, ,﹣1),
,﹣1),
则

 =0.
=0.
所以 ⊥
⊥ =0.
=0.
所以A1B1⊥C1D;
(2)解: ,
,
设 =(x,y,z)为平面MDE的一个法向量.
=(x,y,z)为平面MDE的一个法向量.
则
即 ,
,
令y= ,则x=0,z=1,
,则x=0,z=1,
所以 =(0,
=(0, ,1)
,1)
又 =(0,0,1)为平面DEA的一个法向量,
=(0,0,1)为平面DEA的一个法向量,
所以cos< ,
, >=
>= =
=
所以二面角M﹣DE﹣A的大小为 .
.
A1(1,0,1),B1(0,1,1),C1(0,0,1),D(
 ,
, ,0),
,0), =(﹣1,1,0),
=(﹣1,1,0), =(
=( ,
, ,﹣1),
,﹣1),则


 =0.
=0.所以
 ⊥
⊥ =0.
=0.所以A1B1⊥C1D;
(2)解:
 ,
,设
 =(x,y,z)为平面MDE的一个法向量.
=(x,y,z)为平面MDE的一个法向量.则

即
 ,
,令y=
 ,则x=0,z=1,
,则x=0,z=1,所以
 =(0,
=(0, ,1)
,1)又
 =(0,0,1)为平面DEA的一个法向量,
=(0,0,1)为平面DEA的一个法向量,所以cos<
 ,
, >=
>= =
=
所以二面角M﹣DE﹣A的大小为
 .
.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
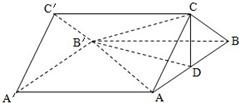 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,