题目内容
设a>1,解关于x的不等式loga(2x2-3x+1)>loga(x2+2x-3).
分析:由a>1,loga(2x2-3x+1)>loga(x2+2x-3),可得2x2-3x+1>x2+2x-3>0,解不等式组可求
解答:解:∵a>1,loga(2x2-3x+1)>loga(x2+2x-3).
∴2x2-3x+1>x2+2x-3>0
∴
解不等式组可得,
∴x>4或x<-3
∴原不等式的解集为:{x|x>4或x<-3}
∴2x2-3x+1>x2+2x-3>0
∴
|
解不等式组可得,
|
∴x>4或x<-3
∴原不等式的解集为:{x|x>4或x<-3}
点评:本题主要考查了利用对数函数的单调性解不等式,二次不等式的求解,解题中要注意,对对数的真数大于0的限制是解题中容易漏掉的考虑.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
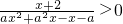 .
.