题目内容
8.已知函数f(x)=x-$\frac{a}{x}$-2lnx,a∈R.(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1,x2,且x1<x2,
①求a的取值范围;
②证明:f(x2)<x2-1.
分析 (1)求出函数的定义域为(0,+∞),函数的导数,令f′(x)=0,①当△≤0,②当△>0进行分类讨论.
(2)①求出函数f(x)有两个极值点x1,x2,等价于方程x2-2x+a=0在(0,+∞),直接推出结果.
②通过(1),(2),推出0<a<1,构造新函数g(t)=t-2lnt-1,1<t<2,利用新函数的单调性证明
求解即可.
解答 (1)解:函数$f(x)=x-\frac{a}{x}-2lnx$的定义域为(0,+∞),$f'(x)=1+\frac{a}{x^2}-\frac{2}{x}=\frac{{{x^2}-2x+a}}{x^2}$,
令f′(x)=0,得x2-2x+a=0,其判别式△=4-4a,
①当△≤0,即a≥1时,x2-2x+a≥0,f′(x)≥0,此时,f(x)在(0,+∞)上单调递增;
②当△>0,即a<1时,方程x2-2x+a=0的两根为${x_1}=1-\sqrt{1-a}$,${x_2}=1+\sqrt{1-a}>1$,
若a≤0,则x1≤0,则x∈(0,x2)时,f′(x)<0,x∈(x2,+∞)时,f′(x)>0,
此时,f(x)在(0,x2)上单调递减,在(x2,+∞)上单调递增;
若a>0,则x1>0,则x∈(0,x1)时,f′(x)>0,x∈(x1,x2)时,f′(x)<0,x∈(x2,+∞)时,f′(x)>0,
此时,f(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)在(0,1+$\sqrt{1-a}$)上单调递减,在(1+$\sqrt{1-a}$,+∞)上单调递增;
当0<a<1时,函数f(x)在(0,1-$\sqrt{1-a}$)上单调递增,在(1-$\sqrt{1-a}$,1+$\sqrt{1-a}$)上单调递减,在(1+$\sqrt{1-a}$,+∞)上单调递增;
当a≥1时,函数f(x)在(0,+∞)上单调递增.
(2)①解:由(1)可知,函数f(x)有两个极值点x1,x2,等价于方程x2-2x+a=0在(0,+∞)有
两不等实根,故0<a<1.
②证明:由上述过程得0<a<1,${x_2}=1+\sqrt{1-a}$,且1<x2<2,$a=-x_2^2+2{x_2}$.$f({x_2})-{x_2}+1={x_2}-\frac{{-x_2^2+2{x_2}}}{x_2}-2ln{x_2}-{x_2}+1={x_2}-2ln{x_2}-1$,
令g(t)=t-2lnt-1,1<t<2,
则$g'(t)=1-\frac{2}{t}=\frac{t-2}{t}$,
由于1<t<2,则g′(t)<0,故g(t)在(1,2)上单调递减.
故g(t)<g(1)=1-2ln1-1=0.
∴f(x2)-x2+1=g(x2)<0.
∴f(x2)<x2-1.
点评 本题考查函数的导数的应用,函数的极值以及函数的单调性的应用,考查分析问题解决问题的能力,转化思想的应用.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案| A. | 相同的离心率 | B. | 相同的焦点 | C. | 相同的顶点 | D. | 相同的长、短轴 |
| A. | $\frac{1}{2}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
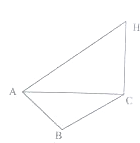 某中学高二研究性学校小组按以下方案测算一种烟花的垂直发射高度:A、B、C三地位于同一水平面上,在C处进行该烟花的垂直发射,观测点A、B两地相距100米,∠BAC=60°,在A地听到地面C处发射声音的时间比B地晚$\frac{2}{17}$秒,在A地测得这种烟花至高点H时的仰角为30°,求这种烟花的垂直发射高度(声音的传播速度为340米/秒)
某中学高二研究性学校小组按以下方案测算一种烟花的垂直发射高度:A、B、C三地位于同一水平面上,在C处进行该烟花的垂直发射,观测点A、B两地相距100米,∠BAC=60°,在A地听到地面C处发射声音的时间比B地晚$\frac{2}{17}$秒,在A地测得这种烟花至高点H时的仰角为30°,求这种烟花的垂直发射高度(声音的传播速度为340米/秒) 如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1.四边形PDCE为矩形,线段PC交DE于点N.
如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1.四边形PDCE为矩形,线段PC交DE于点N.