Question

【题目】已知函数f（x）=ex﹣ax﹣1﹣ ，x∈R．
（Ⅰ）若a= ，求函数f（x）的单调区间；
（Ⅱ）若对任意x≥0都有f（x）≥0恒成立，求实数a的取值范围；
（Ⅲ）设函数F（x）=f（x）+f（﹣x）+2+x2 ， 求证：F（1）F（2）…F（n）＞（en+1+2） （n∈N*）．

Answer 1

【答案】（Ⅰ）解： ，令g（x）=f'（x），则g'（x）=ex﹣1，

则当x∈（﹣∞，0）时，g'（x）＜0，f'（x）单调递减，

当x∈（0，+∞）时，g'（x）＞0，f'（x）单调递增．

所以有 ，所以f（x）在（﹣∞，+∞）上递增…

（Ⅱ）解：当x≥0时，f'（x）=ex﹣x﹣a，令g（x）=f'（x），

则g'（x）=ex﹣1≥0，则f'（x）单调递增，f'（x）≥f'（0）=1﹣a

当a≤1即f'（x）≥f'（0）=1﹣a≥0时，f（x）在（0，+∞）上递增，f（x）≥f（0）=0成立；

当a＞1时，存在x0∈（0，+∞），使f'（x0）=0，

则f（x）在（0，x0）上递减，则当x∈（0，x0）时，f（x）＜f（0）＜0，不合题意．

综上a≤1．

（Ⅲ）证明：∵F（x）=ex+e﹣x，

∴

∴F（1）F（n）＞en+1+2，F（2）F（n﹣1）＞en+1+2

…F（n）F（1）＞en+1+2．

由此得，[F（1）F（2）…F（n）]2=[F（1）F（n）][F（2）F（n﹣1）]…[F（n）F（1）]＞（en+1+2）n

故 （n∈N*）．

【解析】（Ⅰ）求出导函数，对导函数二次求导，得出导函数的最小值为 ＞0，判断原函数递增；（Ⅱ）二次求导，得出导函数递增，对1﹣a进行分类讨论，得出a的范围；（Ⅲ）求出F（x）=ex+e﹣x，利用放缩法判断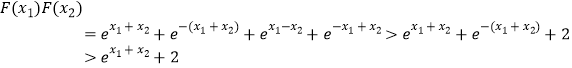

得出F（1）F（n）＞en+1+2，…F（n）F（1）＞en+1+2．最后得出结论．