题目内容

在△ABC中，角A、B、C所对的边分别为a,b,c,且c=10,又知==,求a,b及△ABC的内切圆半径.

解:由=,=,可得=,

变形为sinAcosA=sinBcosB,

∴sin2A=sin2B，

又∵a≠b,

∴2A=π-2B,

∴A+B=，∴△ABC是直角三角形.

由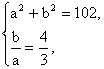

解得a=6,b=8.

所以内切圆半径为r===2.

练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
3
bc，且b=
3
a，则下列关系一定不成立的是（　　）
A、a=c
B、b=c
C、2a=c
D、a2+b2=c2
在△ABC中，角A，B，C的对边分别为a，b，c，已知B=60°，cos（B+C）=-
1114
．
（1）求cosC的值；
（2）若bcosC+acosB=5，求△ABC的面积．
在△ABC中，角A，B，C的对边分别是a，b，c，且bsinA=
3
acosB．
（1）求角B的大小；
（2）若a=4，c=3，D为BC的中点，求△ABC的面积及AD的长度．
在△ABC中，角A、B、C所对的边分别为a、b、c并且满足
b
a
=
sinB
cosA
．
（1）求∠A的值；
（2）求用角B表示
2
sinB-cosC，并求它的最大值．
在△ABC中，角A，B，C所对边的长分别为a，b，c，且a=
5
，b=3，sinC=2sinA，则sinA=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网