题目内容
已知函数 ,若关于x的方程f(x2+2x)=a(a∈R)有六个不同的实根,则a的取值范围是( )
,若关于x的方程f(x2+2x)=a(a∈R)有六个不同的实根,则a的取值范围是( )
|
| A. | (2,8] | B. | (2,9] | C. | (8,9] | D. | (8,9) |
考点:
函数的零点与方程根的关系.
专题:
压轴题;函数的性质及应用.
分析:
令t=x2+2x,则t≥﹣1,f(t)= .由题意可得,函数f(t)的图象与直线y=a 有3个不同的交点,且每个t值有2个x值与之对应,数形结合可得
.由题意可得,函数f(t)的图象与直线y=a 有3个不同的交点,且每个t值有2个x值与之对应,数形结合可得
a的取值范围.
解答:
解:令t=x2+2x,则t≥﹣1,函数f(t)= .
.
由题意可得,函数f(t)的图象与直线y=a 有3个不同的交点,且每个t值有2个x值与之对应,如图所示:
由于当t=﹣1时,f(t)=8,此时,t=﹣1对应的x值只有一个x=﹣1,不满足条件,故a的取值范围是 (8,9],
故选C.

点评:
本题主要考查函数的零点与方程的根的关系,体现了数形结合的数学思想及等价转化的数学思想,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( ) ,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )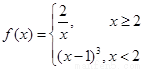 ,若关于x的方程
,若关于x的方程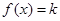 有两个不同的实根,则实数k的取值范围是
.
有两个不同的实根,则实数k的取值范围是
.  若关于x的方程
若关于x的方程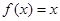 有且仅有二个不等实根,则实数a的取值范围是( )
有且仅有二个不等实根,则实数a的取值范围是( ) B.(
B.( ) C.
) C. D.(-3,-2]
D.(-3,-2]