题目内容
已知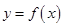 为
为 上的可导函数,当
上的可导函数,当 时,
时, ,则关于x的函数
,则关于x的函数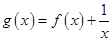 的零点个数为( )
的零点个数为( )
A.1 B.2 C.0 D.0或 2
【答案】
C
【解析】 ,且
,且 ,
,
令 ,故无解。
,故无解。
>0时,xf'(x) + f(x) = (xf(x))' >0,或者xf(x)是x的严格递增函数,由于 ,且xf(x) > 0f(0) = 0,所以
,且xf(x) > 0f(0) = 0,所以 对任何大于零的x成立,所以显然在x轴正半轴不可能有零点;x<0时,已知条件就是在说 xf'(x) + f(x) < 0,或者xf(x)是x的严格递减函数,所以还是有xf(x) > 0f(0) = 0 (x<0),也就是说,
对任何大于零的x成立,所以显然在x轴正半轴不可能有零点;x<0时,已知条件就是在说 xf'(x) + f(x) < 0,或者xf(x)是x的严格递减函数,所以还是有xf(x) > 0f(0) = 0 (x<0),也就是说, (注意x是负的,所以不等号要变号).此时
(注意x是负的,所以不等号要变号).此时 总是负数,小于
总是负数,小于 是不可能与x轴有交点的。所以没有零点。
是不可能与x轴有交点的。所以没有零点。


练习册系列答案
相关题目
 为
为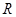 上的可导函数,当
上的可导函数,当 时,
时, ,则关于
,则关于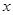 的函数
的函数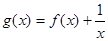 的零点个数为( )
的零点个数为( )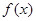 为
为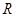 上的可导函数,且
上的可导函数,且 ,均有
,均有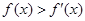 ,则有( )
,则有( ) ,
,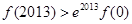
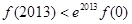
 ,
, 为
为 上的可导函数,且
上的可导函数,且 ,均有
,均有 ,则有( )
,则有( )


