题目内容
已知函数 满足
满足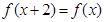 ,当
,当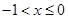 时
时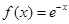 ;当
;当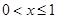 时
时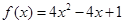 .
.
(Ⅰ)求函数 在(-1,1)上的单调区间;
在(-1,1)上的单调区间;
(Ⅱ)若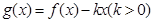 ,求函数
,求函数 在
在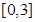 上的零点个数.
上的零点个数.
(Ⅰ) 单调递减区间为 ,递增区间为
,递增区间为 ; (Ⅱ)参考解析
; (Ⅱ)参考解析
解析试题分析:(Ⅰ)因为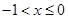 时,函数
时,函数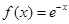 是单调递减的,
是单调递减的,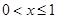 时,函数
时,函数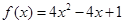 的图像的对称轴是
的图像的对称轴是 ,开口向上.所以
,开口向上.所以 递减,
递减, 的递增.又因为当
的递增.又因为当 .所以综上可得函数的单调递减区间为
.所以综上可得函数的单调递减区间为 ,递增区间为
,递增区间为 .
.
(Ⅱ)因为函数 满足
满足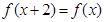 即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为
即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为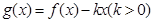 ,求函数
,求函数 在
在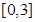 上的零点个数.即等价于求方程
上的零点个数.即等价于求方程 的根的个数.即等价于
的根的个数.即等价于 .即等价于函数
.即等价于函数 与
与 的图像的交点个数.所以通过如图所示即可解得结论.
的图像的交点个数.所以通过如图所示即可解得结论.
试题解析:(1)由题可知
由图可知,函数 在
在 的单调递减区间为
的单调递减区间为 ,
,
在 递增区间为
递增区间为 6分
6分
考察数形结合思想
(2)当 时,
时, 有1个零点 8分
有1个零点 8分
当 时,
时, 有2个零点 10分
有2个零点 10分
当 时,
时, 有3个零点 12分
有3个零点 12分
当 时,
时, 有4个零点 13分
有4个零点 13分
考点:1.函数的周期性.2.分段函数的性质.3.函数图像解题的思想.4.分类,归纳的思想.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
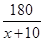 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=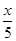 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).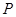 的关系允许近似的满足:
的关系允许近似的满足: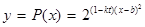 (其中
(其中 为关税的税率,且
为关税的税率,且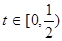 ,
, 为市场价格,
为市场价格,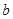 、
、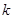 为正常数),当
为正常数),当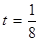 时的市场供应量曲线如图:
时的市场供应量曲线如图: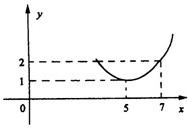
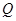 ,它近似满足
,它近似满足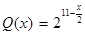 .当
.当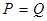 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率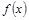 与第x天近似地满足
与第x天近似地满足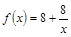 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费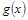 近似地满足
近似地满足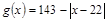 (元).
(元).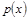 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,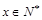 )的函数关系;
)的函数关系;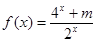 是奇函数.
是奇函数.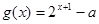 .若函数
.若函数 与
与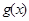 的图象至少有一个公共点.求实数a的取值范围.
的图象至少有一个公共点.求实数a的取值范围. 。
。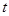 小时内供水总量为
小时内供水总量为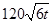 吨(
吨(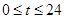 ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?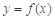 满足:当
满足:当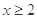 时,
时,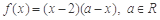 ,当
,当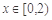 时,
时,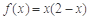 .
.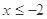 时,
时,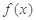 的表达式;
的表达式;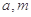 满足什么条件时,函数
满足什么条件时,函数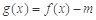 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.