题目内容
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=![]() ,EF=EC=1,
,EF=EC=1,
⑴求证:平面BEF⊥平面DEF;
⑵求二面角A-BF-E的大小。

(1)见解析
(2)二面角的大小为![]()
解析:
①证明: ∵平面ACEF⊥平面ABCD,EC⊥AC,
∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∵正方形ABCD的边长为![]() ,∴AC=BD=2;
,∴AC=BD=2;
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1;易求得DF=BF=![]() ,
,
DE=BE=![]() ,由勾股定理知 DF⊥EF,BF⊥EF,
,由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角,
 由BF=DF=
由BF=DF=![]() ,BD=2可知∠BFD=
,BD=2可知∠BFD=![]() ,
,
∴平面BEF⊥平面DEF ………………(6分)
⑵取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=![]() ,∴AM⊥BF,
,∴AM⊥BF,
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角。
易求得![]() ,
,![]() ;
;
在Rt△![]() 中,可求得
中,可求得![]() ,
,
 ∴在△
∴在△![]() 中,由余弦定理求得
中,由余弦定理求得![]() ,
,
∴![]() ……………………………(12分)
……………………………(12分)
解法2:⑴∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD;
建立如图所示的空间直角坐标系C-xyz,则![]()

![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() …(2分)
…(2分)
设平面BEF、平面DEF的法向量分别为
![]() ,则
,则
![]() ①
①
![]() ②,
②,![]() ③,
③, ![]() ④.
④.
由①③③④解得![]() ,∴
,∴![]() ,…(4分)
,…(4分)
∴![]() ,∴
,∴![]() ,故平面BEF⊥平面DEF…………(6分)
,故平面BEF⊥平面DEF…………(6分)
⑵设平面ABF的法向量为![]() ,∵
,∵![]() ,
,![]()
∴![]() ,
,![]() ,解得
,解得![]()
∴![]() ,………(8分)∴
,………(8分)∴![]() ……(10分)
……(10分)
由图知,二面角A-BF-E的平面角是钝角,故所求二面角的大小为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
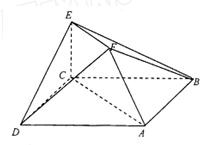 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=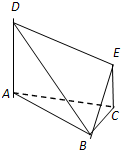 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.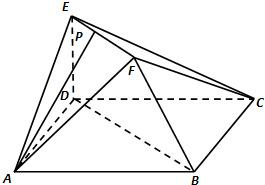 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.