题目内容
函数y=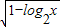
的定义域为（ ）A．{x|0＜x＜1}
B．{x|0＜x≤1}
C．{x|x＞0}
D．{x|0＜x≤2}
【答案】分析：令1-log2x≥0，即可解出函数定义域》
解答：解：由1-log2x≥0，解得0＜x≤2，
所以函数y=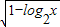
的定义域为{x|0＜x≤2}．
故选D．
点评：本题考查函数的定义域及其求法，属基础题，难度不大．
解答：解：由1-log2x≥0，解得0＜x≤2，
所以函数y=
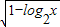的定义域为{x|0＜x≤2}．故选D．
点评：本题考查函数的定义域及其求法，属基础题，难度不大．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
的定义域为R,则k的取值范围是______________.
的定义域为（ ）
的定义域为（ ）
的定义域为（ ）
}
，+∞）
）
，+∞）
的定义域为 ．