Question

在平面直角坐标系xOy中，有一个以F₁（0，-）和F₂（0，）为焦点、离心率为的椭圆.设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的交点分别为A、B，且向量.求：

（1）点M的轨迹方程；

（2）的最小值.

Answer 1

解：(1 )椭圆方程可写为=1（a＞b＞0）,且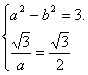

得a²=4,b²=1,所以曲线C的方程为x²+=1(x＞0,y＞0).

y=(0＜x＜1),

y′=-.

设P(x₀,y₀),因P在C上,有0＜x₀＜1,y₀=,y′|_x=x0=,得切线AB的方程为y=(x-x₀)+y₀.

设A(x,0)和B(0,y),由切线方程得x=,y=.

由得M的坐标为(x,y),由x₀、y₀满足C的方程,

∴点M的轨迹方程为=1(x＞1,y＞2).

(2)∵=x²+y²,y²=，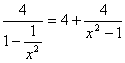

∴=x²-1+ +5≥4+5=9.且当x²-1=,即x=＞1时,上式取等号.

故的最小值为3.