题目内容
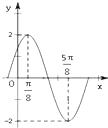
【题目】已知函数f（x）=Asin（ωx+φ）（其中A＞0， 
）的图象如图所示． 
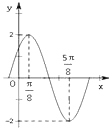
（1）求A，w及φ的值；
（2）若tana=2，求 
的值．
【答案】
（1）解：由图知A=2，
T=2（ 
）=p，
∴w=2，
∴f（x）=2sin（2x+φ）
又∵ 
=2sin（ 
+φ）=2，
∴sin（ +φ）=1，
∴ +j= 
，φ= +2kπ，
∵ 
，
∴φ=
（2）解：由（1）知：f（x）=2sin（2x+ ），
∴ 
=2sin（2a+ 
）=2cos2a=4cos2a﹣2
∵tana=2，
∴sina=2cosa，
又∵sin2a+cos2a=1，
∴cos2a= 
，
∴ = 
【解析】（1）根据函数图象的最大值和最小值确定A的值，由周期可知ω的值，最后再代入特殊值可确定φ的值．（2）先表示出f（α+ 
）的表达式，根据tana=2求出cos2a的值代入即可得到答案．
练习册系列答案
中考解读考点精练系列答案
相关题目
