题目内容
等差数列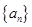 前
前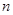 项和
项和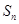 ,若
,若 ,则
,则 __________.
__________.
解析试题分析:法一:设该等差数列首项、公差分别为 ,则由
,则由 可得
可得 ,化简得
,化简得 ,所以
,所以 ;
;
法二:由 可得
可得 即
即 ,所以
,所以 即
即 ,从而
,从而 ,所以
,所以 ;
;
法三:因为数列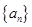 是等差数列,且
是等差数列,且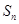 为其前
为其前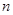 项和,所以
项和,所以 也成等差数列,所以
也成等差数列,所以 ,又因为
,又因为 ,所以
,所以 ,所以
,所以 ;
;
法四:由 可知,该等差数列的公差不为0,而等差数列的前
可知,该等差数列的公差不为0,而等差数列的前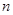 项和的形式为
项和的形式为 ,其中
,其中 为公差的一半,由
为公差的一半,由 可知
可知 的对称轴为
的对称轴为 ,所以
,所以 即
即 ,所以
,所以 ,从而
,从而 .
.
考点:等差数列的前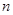 项和.
项和.

练习册系列答案
相关题目
 满足
满足 则
则 .
. 为等差数列,
为等差数列, 为其前n项和,则使得
为其前n项和,则使得 达到最大值的n等于 .
达到最大值的n等于 . 的通项公式为
的通项公式为 ,下列四个命题.
,下列四个命题. :数列
:数列 :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列;
是递增数列; :数列
:数列 是递增数列.其中真命题的是 .
是递增数列.其中真命题的是 . 是等差数列,
是等差数列, ,
, ,设
,设 ,则数列
,则数列 的通项公式
的通项公式
 是递增的等差数列,
是递增的等差数列, ,
,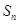 为其前
为其前 项和,若
项和,若 成等比数列,则
成等比数列,则 .
.