题目内容
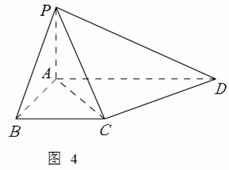
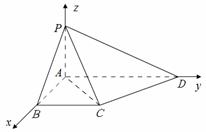
如图4,在四棱锥![]() ,
,![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 是直角梯形中,
是直角梯形中,![]() .
.
(1)求证: ![]() 平面
平面![]() ;(2)求二面角
;(2)求二面角![]() 的余弦值.
的余弦值.
(1)证明:∵![]() 平面
平面![]() , ∴
, ∴![]() .(1分)
.(1分)
又∵![]() ,∴
,∴![]() (2分)
(2分)
过C作![]() ,交AD于E,则
,交AD于E,则![]() (3分)
(3分)
∴![]() ,(4分)
,(4分)
在![]() 中,
中,![]() ,∴
,∴![]() .(5分)
.(5分)
又∵![]() ,∴
,∴![]() 平面
平面![]() .(6分)
.(6分)
(2)(方法一)∵![]() ,∴
,∴![]() 平面
平面![]() .(7分)
.(7分)
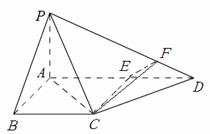
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,可知
,可知![]() . (8分)
. (8分)
∴![]() 是二面角
是二面角![]() 的平面角. (9分)
的平面角. (9分)
设![]() ,则
,则![]() ,
,![]() .
.
![]() ∽
∽![]() ,
,![]() ,
,![]() . (11分)
. (11分)
∴![]() , (12分)
, (12分)
∴![]() .即二面角
.即二面角![]() 的余弦值为
的余弦值为![]() . (14分)
. (14分)
(方法二)如图建立空间直角坐标系,设![]() ,则
,则![]()
∴![]() , (7分)
, (7分)
![]() , (8分)
, (8分)
设平面![]() 的法向量为
的法向量为![]() ,
,
则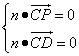 ,即
,即![]() 化简得
化简得![]()
令![]() ,得
,得![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量. (10分)
的一个法向量. (10分)
又平面ACD的一个法向量为![]() (11分)
(11分)
设向量![]() 和
和![]() 所成角为
所成角为![]() ,则
,则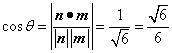 (13分)
(13分)
∴即二面角![]() 的余弦值为
的余弦值为![]() . (14分)
. (14分)

练习册系列答案
相关题目
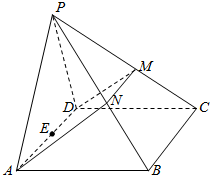 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.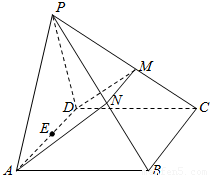
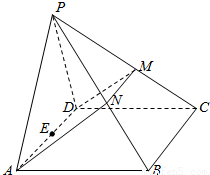 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.