题目内容
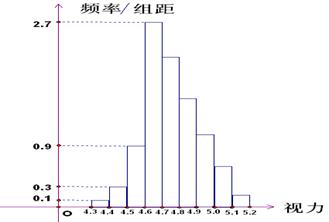
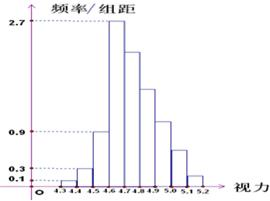 为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如图所示,已知后6组的频数从左到右依次是等差数列an的前六项.
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如图所示,已知后6组的频数从左到右依次是等差数列an的前六项.(1)试确定视力介于4.9至5.0的抽查学生的人数.
(2)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率μ的大小.
分析:(1)由频率分布直方图分析可得,等差数列an的a1,前六项和S6,设公差为d,根据等差数列的前n项和公式求解d=-5,从而得出a4即视力介于4.9至5.0的抽查学生的人数.
(2)由(1)知视力低于5.0的学生总数,从而得出其频率:μ=
=0.91,利用样本的频率分布估计总体分布
即可估计该校新生近视率.
(2)由(1)知视力低于5.0的学生总数,从而得出其频率:μ=
| 91 |
| 100 |
即可估计该校新生近视率.
解答:解:(1)由题意知,a1=2.7×0.1×100=27,an前六项和S6=100-(0.1+0.3+0.9)×0.1×100=87
设公差为d∴27×6+
d=87∴d=-5,∴a4=a1+3d=27-15=12
所以视力介于4.9至5.0的抽查学生的人数为12人.
(2)由(1)知视力低于5.0的学生总数为1+3+9+27+22+17+12=91∴μ=
=0.91
∴估计该校新生近视率为91%
设公差为d∴27×6+
| 6×(6-1) |
| 2 |
所以视力介于4.9至5.0的抽查学生的人数为12人.
(2)由(1)知视力低于5.0的学生总数为1+3+9+27+22+17+12=91∴μ=
| 91 |
| 100 |
∴估计该校新生近视率为91%
点评:本题考查读频率分布直方图的能力、利用统计图获取信息的能力和数列的简单应用,是一道频率分布直方图与等差数列交汇的题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 的前4项,后6组的频数从左到右依次是等差数列
的前4项,后6组的频数从左到右依次是等差数列 的前6项.
的前6项.
 的大小.
的大小.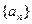 的
的 前六项。
前六项。 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率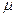 的大
的大
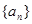 的前六项。
的前六项。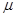 的大
的大