题目内容
在由1,2,3,4,5组成可重复数字的三位数中任取一个数.
(Ⅰ) 求取出的数各位数字互不相同的概率;
(Ⅱ) 记ξ为组成这个数的各位数字中不同的偶数个数(例如:若这个数为212,则ξ=1).求随机变量ξ的分布列及其数学期望Eξ.
解:(Ⅰ)由题意知本题是一个等可能事件的概率,
试验发生包含的事件数53,
满足条件的事件数A53,
记“取出的数各位数字互不相同”为事件B,
∴P(B)= .…(5分)
.…(5分)
(Ⅱ) 随机变量ξ的取值为0,1,2.
P(ξ=0)=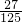 ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)=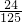
∴ξ的分布列是
所以ξ的数学期望Eξ=0×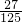 +1×
+1× +2×
+2×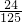 =
= .…(13分)
.…(13分)
分析:(Ⅰ)本题是一个等可能事件的概率,试验发生包含的事件数53,满足条件的事件数A53,根据等可能事件的概率公式得到结果.
(Ⅱ)由题意知变量的可能取值是0,1,2,结合变量对应的事件和等可能事件的概率公式写出变量的概率,写出分布列和做出期望值.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是正确理解“记ξ为组成这个数的各位数字中不同的偶数个数”和变量对应的事件的意义.
试验发生包含的事件数53,
满足条件的事件数A53,
记“取出的数各位数字互不相同”为事件B,
∴P(B)=
 .…(5分)
.…(5分)(Ⅱ) 随机变量ξ的取值为0,1,2.
P(ξ=0)=
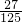 ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)=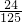
∴ξ的分布列是
| ξ | 0 | 1 | 2 |
| P | 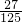 |  | 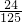 |
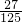 +1×
+1× +2×
+2×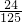 =
= .…(13分)
.…(13分)分析:(Ⅰ)本题是一个等可能事件的概率,试验发生包含的事件数53,满足条件的事件数A53,根据等可能事件的概率公式得到结果.
(Ⅱ)由题意知变量的可能取值是0,1,2,结合变量对应的事件和等可能事件的概率公式写出变量的概率,写出分布列和做出期望值.
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是正确理解“记ξ为组成这个数的各位数字中不同的偶数个数”和变量对应的事件的意义.

练习册系列答案
相关题目