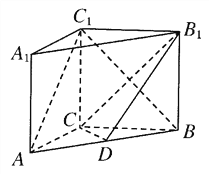
题目内容
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使
折起,使![]() 间的距离为
间的距离为![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为( )
的距离为( )
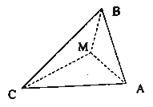
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
【答案】A
【解析】由已知得AB=2,AM=MB=MC=1,BC=![]() ,
,
由△AMC为等边三角形,取CM中点D,则AD⊥CM,AD交BC于E,则AD=![]() ,DE=
,DE=![]() ,CE=
,CE=![]() .
.
折起后,由BC2=AC2+AB2,知∠BAC=90,
又cos∠ECA=![]() ,∴AE2=CA2+CE22CACEcos∠ECA=
,∴AE2=CA2+CE22CACEcos∠ECA=![]() ,于是AC2=AE2+CE2.
,于是AC2=AE2+CE2.
∴∠AEC=90.
∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥ABCM的高,AE=![]()
设点M到面ABC的距离为h,则
∵S△BCM=![]()
∴由VABCM=VMABC,可得![]() ×
×![]() ×
×![]() =
=![]() ×
×![]() ×
×![]() ×1×h,∴h=
×1×h,∴h=![]()
故选A.

【题目】某公司为确定下一年投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年利润y(单位:万元)的影响,对近5年的宣传费xi和年利润yi(i=1,2,3,4,5)进行了统计,列出了下表:
x(单位:千元) | 2 | 4 | 7 | 17 | 30 |
y(单位:万元) | 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合y与x的关系,请你建立y关于x的线性回归方程(系数精确到0.01);
(2)小李决定选择对数回归模拟拟合y与x的关系,得到了回归方程: ![]() =1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据
=1.450lnx+0.024,并提供了相关指数R2=0.995,请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润(精确到0.01)(小王也提供了他的分析数据 ![]() (yi﹣
(yi﹣ ![]() i)2=1.15) 参考公式:相关指数R2=1﹣
i)2=1.15) 参考公式:相关指数R2=1﹣ 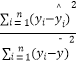
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ![]() =
= 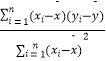 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x,参考数据:ln40=3.688,
x,参考数据:ln40=3.688, ![]() =538.
=538.