题目内容

已知a⊥α,a⊥b,bα,求证：b∥α.

思路分析：因为bα,故只要用共面向量定理证明b、m、n共面即可.

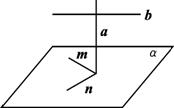
证明：在α内作不共线向量m、n,

∵a、m、n不共面，∴b=xa+ym+zn,

两边同乘a,得a·b=xa·a+ya·m+za·n.

∵a⊥b,a⊥m,a⊥n,

∴a·b=0,a·m=0,a·n=0，得xa·a=0.

而a≠0,∴x=0,即b=ym+zn.

∴b、m、n为共面向量.

又bα,∴b∥α.


练习册系列答案
相关题目
（1）选修4-2：矩阵与变换
已知矩阵M=（
2a
2b
）的两^E值分别为λ1=-1和λ2=4．
（I）求实数的值；
（II ）求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程．
（2）选修4-4：坐标系与参数方程
在直角坐标平面内，以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系．已知曲线C的参数方程为
x=sinα
y=2cos2α-2
，
（a为餓），曲线D的鍵标方程为ρsin（θ-
π
4
）=-
3
2
2
．
（I ）将曲线C的参数方程化为普通方程；
（II）判断曲线c与曲线D的交点个数，并说明理由．
（3）选修4-5：不等式选讲
已知a，b为正实数．
（I）求证：
a2
b
+
b2
a
≥a+b；
（II）利用（I）的结论求函数y=
(1-x)2
x
+
x2
1-x
（0＜x＜1）的最小值．
已知a＞b＞0，那么下列不等式成立的是（　　）
（2012•杭州一模）已知向量a=(cos
3x
2
，sin
3x
2
)，b=(cos
x
2
，-sin
x
2
)， x∈[0， 
π
2
]．
（Ⅰ）求
a
•
b
及|
a
+
b
|；
（Ⅱ）若函数f（x）=
a
•
b
-2t|
a
+
b
|的最小值为-
3
2
，求t的值．
已知a，b，c，d为实数，判断下列命题的真假．
（1）若ac2＞bc2，则a＞b
（2）若a＜b＜c，则 a2＞ab＞b2
（3）若a＞b＞0，则
a
d
＞
b
c

（4）若0＜a＜b，则 
b
a
＜
b+x
a+x
．

已知A={a，b，c}，B={－1，0，1}，映射f：A→B满足f(a)＋f(b)=f(c)，求映射f：A→B的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网