题目内容
已知命题p:关于并的方程戈x2-x+a=0无实根,命题q:关于x的函数y=-x2-ax+1在[-1,+∞)上是减函数.若?q是真命题,p∨q是真命题,则实数a的取值范围是( )
| A.[2,+∞) | B.[
| C.(
| D.(-∞,
|
若命题p为真,则有△=1-4a<0,解得a>
,即p:a>
.
若命题q为真,则有-
≤-1,解得a≥2.若?q是真命题,则q为假命题,又p∨q是真命题,所以p为真命题.
即
,解得
<a<2,即实数a的取值范围是(
,2).
故选C.
| 1 |
| 4 |
| 1 |
| 4 |
若命题q为真,则有-
| a |
| 2 |
即
|
| 1 |
| 4 |
| 1 |
| 4 |
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
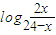 图象对称中心的坐标;
图象对称中心的坐标; ,+∞)
,+∞) ,2)
,2) )∪(2,+∞)
)∪(2,+∞)