题目内容
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为
,各局比赛的结果都相互独立,第1局甲当裁判.
(I)求第4局甲当裁判的概率;
(II)求前4局中乙恰好当1次裁判概率.
| 1 | 2 |
(I)求第4局甲当裁判的概率;
(II)求前4局中乙恰好当1次裁判概率.
分析:(I)设A1表示事件“第二局结果为甲胜”,A2表示事件“第三局甲参加比赛结果为甲负”,A表示事件“第四局甲当裁判”,可得A=A1•A2.利用相互独立事件的概率计算公式即可得出;
(II)设B1表示事件“第一局比赛结果为乙胜”,B2表示事件“第二局乙参加比赛结果为乙胜”,B3表示事件“第三局乙参加比赛结果为乙胜”,B表示事件“前4局中乙恰好当1次裁判”.可得B=
•B3+B1•B2•
+B1•
,利用互斥事件和相互独立事件的概率计算公式即可得出.
(II)设B1表示事件“第一局比赛结果为乙胜”,B2表示事件“第二局乙参加比赛结果为乙胜”,B3表示事件“第三局乙参加比赛结果为乙胜”,B表示事件“前4局中乙恰好当1次裁判”.可得B=
. |
| B1 |
. |
| B3 |
. |
| B2 |
解答:解:(I)设A1表示事件“第二局结果为甲胜”,A2表示事件“第三局甲参加比赛结果为甲负”,A表示事件“第四局甲当裁判”.
则A=A1•A2.
P(A)=P(A1•A2)=P(A1)P(A2)=
×
=
.
(II)设B1表示事件“第一局比赛结果为乙胜”,B2表示事件“第二局乙参加比赛结果为乙胜”,
B3表示事件“第三局乙参加比赛结果为乙胜”,B表示事件“前4局中乙恰好当1次裁判”.
则B=
•B3+B1•B2•
+B1•
,
则P(B)=P(
•B3+B1•B2•
+B1•
)
=P(
•B3)+P(B1•B2•
)+P(B1•
)
=P(
)P(B3)+P(B1)P(B2)P(
)+P(B1)P(
)
=
+
+
=
.
则A=A1•A2.
P(A)=P(A1•A2)=P(A1)P(A2)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(II)设B1表示事件“第一局比赛结果为乙胜”,B2表示事件“第二局乙参加比赛结果为乙胜”,
B3表示事件“第三局乙参加比赛结果为乙胜”,B表示事件“前4局中乙恰好当1次裁判”.
则B=
. |
| B1 |
. |
| B3 |
. |
| B2 |
则P(B)=P(
. |
| B1 |
. |
| B3 |
. |
| B2 |
=P(
. |
| B1 |
. |
| B3 |
. |
| B2 |
=P(
. |
| B1 |
. |
| B3 |
. |
| B2 |
=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 8 |
点评:正确理解题意和熟练掌握相互独立事件和互斥事件的概率计算公式是解题的关键.

练习册系列答案
相关题目
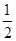 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.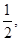 各局比赛的结果都相互独立,第
各局比赛的结果都相互独立,第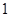 局甲当裁判.
局甲当裁判.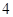 局甲当裁判的概率;
局甲当裁判的概率; ,各局比赛的结果都相互独立,第1局甲当裁判.
,各局比赛的结果都相互独立,第1局甲当裁判.