题目内容
已知M,N为平面区域
内的两个动点,向量
=(1,3)则
•
的最大值是
|
| a |
| MN |
| a |
40
40
.分析:根据向量数量积的几何意义,得当向量
与
方向相同且
的模最大时,
•
最大,画出平面区域
表示的图形,数形结合不难得出
•
的最大值,从而得到本题的答案.
| MN |
| a |
| MN |
| MN |
| a |
|
| MN |
| a |
解答: 解:作出不等式组
解:作出不等式组
对应的平面区域,
如图中阴影部分三角形,
由
得M′(0,-6),
由
得N′(4,6).
结合图形得,当
=(4,12)时,
•
的最大值为:(4,12)•(1,3)=4+12×3=40,
故答案为:40.
 解:作出不等式组
解:作出不等式组
|
如图中阴影部分三角形,
由
|
由
|
结合图形得,当
| MN |
| MN |
| a |
故答案为:40.
点评:本题给出平面区域内的两个点N、M,求数量积的最大值,着重考查了平面向量数量积的坐标运算和简单的线性规划等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
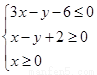 内的两个动点向量
内的两个动点向量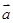 =(1,3)则
=(1,3)则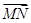 ·
· 内的两个动点,向量
内的两个动点,向量 则
则 的最大值是 .
的最大值是 .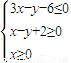 内的两个动点,向量
内的两个动点,向量 则
则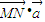 的最大值是 .
的最大值是 .