题目内容
设f(x)是定义在(-∞,+∞)上的函数,对一切x∈R均有f(x)+f(x+2)=0,当-1<x≤1时,f(x)=2x-1,求当1<x≤3时,函数f(x)的解析式.
解:设1<x≤3,则-1<x-2≤1,又对任意的x,有f(x)+f(x+2)=0,
∴f(x+2)=-f(x).
∴f(x-2)=-f[(x-2)+2]=-f(x).
又-1<x-2≤1时,f(x-2)=2(x-2)-1=2x-5,
∴f(x)=-f(x-2)=-2x+5(1<x≤3).
讲评:将1<x≤3转化成-1<x-2≤1,再利用已知条件是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 >0.
>0. )<f(x-
)<f(x- );
); ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(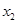 ),则(0,
),则(0, f(
f( 为含峰区间:
为含峰区间: ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r: 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)