题目内容

偶函数f（x）=ax²-2bx+1在（-∞，0]上递增，比较f（a-2）与f（b+1）的大小关系（）
A．f（a-2）＞f（b+1）
B．f（a-2）＜f（b+1）
C．f（a-2）=f（b+1）
D．f（a-2）与f（b+1）大小关系不确定

【答案】分析：根据偶函数f（x）=ax²-2bx+1在（-∞，0]上递增，可知a＜0，b=0，从而a-2＜-2，b+1=1，进而可得f（a-2）＜f（b+1）．
解答：解：∵偶函数f（x）=ax²-2bx+1在（-∞，0]上递增，
∴a＜0，b=0
∴a-2＜-2，b+1=1
∵偶函数f（x）=ax²-2bx+1在（-∞，0]上递增，
∴f（a-2）＜f（-2）＜f（-1）=f（1）=f（b+1）
即f（a-2）＜f（b+1）
故选B．
点评：本题重点考查函数的单调性，考查函数的奇偶性，解题的关键是判断a＜0，b=0．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

（2013•宁波二模）设函数f（x）=

-1，-2≤x≤0

x-1，0＜x≤2

，若函数g（x）=f（x）-ax，x∈[-2，2]为偶函数，则实数a的值为

已知定义域为R的偶函数f（x）=a^x+b•a^-x（a＞0，a≠1，b∈R）．
（1）求实数b的值；
（2）判断并证明f（x）的单调性；
（3）若f((log2x)2-log2x+1)≥f(m+log

x2)对任意x∈[2，4]恒成立，求实数m的取值范围．

已知定义域为R的偶函数f（x）=a^x+b•a^-x（a＞0，a≠1，b∈R）．
（1）求实数b的值；
（2）判断并证明f（x）的单调性；
（3）若 $数学公式$ 对任意x∈[2，4]恒成立，求实数m的取值范围．

已知定义域为R的偶函数f（x）=a^x+b•a^-x（a＞0，a≠1，b∈R）．
（1）求实数b的值；
（2）判断并证明f（x）的单调性；
（3）若f((log2x)2-log2x+1)≥f(m+log

x2)对任意x∈[2，4]恒成立，求实数m的取值范围．

已知定义域为R的偶函数f（x）=a^x+b•a^-x（a＞0，a≠1，b∈R）．
（1）求实数b的值；
（2）判断并证明f（x）的单调性；
（3）若

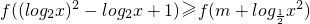对任意x∈[2，4]恒成立，求实数m的取值范围．