题目内容
已知全集U=R,设集合A={x|y=ln(2x-1)},集合B={y|y=sin(x-1)},则(?UA)∩B为( )
分析:求出集合A中函数的定义域确定出A,求出集合B中函数的值域确定出B,求出A的补集,找出A补集与B的交集即可.
解答:解:集合A中的函数y=ln(2x-1),2x-1>0,即x>
,
∴A=(
,+∞),
∵全集U=R,
∴?UA=(-∞,
],
集合B中的函数y=sin(x-1),-1≤y≤1,
∴B=[-1,1],
则(?UA)∩B=[-1,
].
故选C
| 1 |
| 2 |
∴A=(
| 1 |
| 2 |
∵全集U=R,
∴?UA=(-∞,
| 1 |
| 2 |
集合B中的函数y=sin(x-1),-1≤y≤1,
∴B=[-1,1],
则(?UA)∩B=[-1,
| 1 |
| 2 |
故选C
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
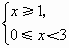 的解集为A,则
的解集为A,则 ,C={x|x2+2ax+2≤0}.
,C={x|x2+2ax+2≤0}. ,C={x|x2+2ax+2≤0}.
,C={x|x2+2ax+2≤0}.