题目内容
动点P(a,b)在不等式组为: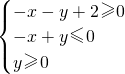 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则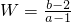 的取值范围是 ________.
的取值范围是 ________.
(-∞,-2]∪[2,+∞)
分析:根据条件画出可行域,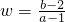 ,再利用几何意义求最值,只需求出可行域内点和点(1,2)连线的斜率的最值,从而得到w的取值范围即可.
,再利用几何意义求最值,只需求出可行域内点和点(1,2)连线的斜率的最值,从而得到w的取值范围即可.
解答: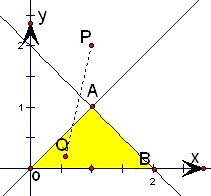 解:根据约束条件画出可行域,
解:根据约束条件画出可行域,
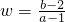 ,表示可行域内点Q和点P(1,2)连线的斜率的最值,
,表示可行域内点Q和点P(1,2)连线的斜率的最值,
当Q点在原点O时,直线PQ的斜率为2,当Q点在可行域内的点B处时,直线PQ的斜率为-2,
结合直线PQ的位置可得,当点Q在可行域内运动时,其斜率的取值范围是:
(-∞,-2]∪[2,+∞)
从而得到w的取值范围(-∞,-2]∪[2,+∞).
故答案为:(-∞,-2]∪[2,+∞).
点评:本题主要考查了简单的线性规划,以及利用分式函数的几何意义为可行域内的点(x,y)和另一个定点的直线斜率求最值,属于基础题.
分析:根据条件画出可行域,
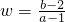 ,再利用几何意义求最值,只需求出可行域内点和点(1,2)连线的斜率的最值,从而得到w的取值范围即可.
,再利用几何意义求最值,只需求出可行域内点和点(1,2)连线的斜率的最值,从而得到w的取值范围即可.解答:
 解:根据约束条件画出可行域,
解:根据约束条件画出可行域,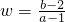 ,表示可行域内点Q和点P(1,2)连线的斜率的最值,
,表示可行域内点Q和点P(1,2)连线的斜率的最值,当Q点在原点O时,直线PQ的斜率为2,当Q点在可行域内的点B处时,直线PQ的斜率为-2,
结合直线PQ的位置可得,当点Q在可行域内运动时,其斜率的取值范围是:
(-∞,-2]∪[2,+∞)
从而得到w的取值范围(-∞,-2]∪[2,+∞).
故答案为:(-∞,-2]∪[2,+∞).
点评:本题主要考查了简单的线性规划,以及利用分式函数的几何意义为可行域内的点(x,y)和另一个定点的直线斜率求最值,属于基础题.

练习册系列答案
相关题目
 已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示.
已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示. 。
。 。
。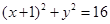 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且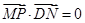 .
.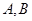 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线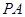 与
与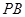 的斜率分别为
的斜率分别为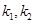 ,证明:
,证明: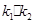 为定值;
为定值;