题目内容
平面内,若三条射线OA、OB、OC两两成等角为?,则?=
.类比该特性:在空间,若四条射线OA、OB、OC、OD两两成等角为θ,则θ=
| 2π |
| 3 |
π-arccos(
)
| 1 |
| 3 |
π-arccos(
)
.| 1 |
| 3 |
分析:这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知平面内,若三条射线OA、OB、OC两两成等角为?,则?=
,我们可类比推理出在空间,若四条射线OA、OB、OC、OD两两成等角为θ,则θ=π-arccos(
).
| 2π |
| 3 |
| 1 |
| 3 |
解答:解:∵“平面内,若三条射线OA、OB、OC两两成等角为?,则?=
”
我们可类比推理出:
在空间,若四条射线OA、OB、OC、OD两两成等角为θ,则θ=π-arccos(
).
故答案为:π-arccos(
).
| 2π |
| 3 |
我们可类比推理出:
在空间,若四条射线OA、OB、OC、OD两两成等角为θ,则θ=π-arccos(
| 1 |
| 3 |
故答案为:π-arccos(
| 1 |
| 3 |
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
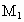 、
、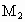 与
与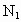 、
、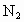 ,则三角形面积之比
,则三角形面积之比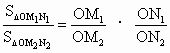 ,若从点O所作的不在一平面内的三条射线OP、OQ和OR上,分别有
,若从点O所作的不在一平面内的三条射线OP、OQ和OR上,分别有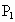 、
、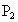 ,点
,点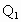 、
、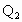 和点
和点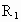 、
、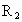 ,则类似的结论为___________.
,则类似的结论为___________.
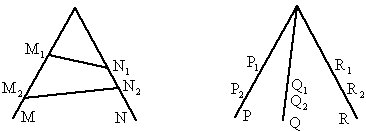
 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .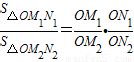 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .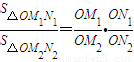 .若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .
.若从点O所作的不在同一个平面内的三条射线OP,OQ和OR上分别有点P1,P2与点Q1,Q2和R1,R2,则类似的结论为: .