题目内容
已知函数f(x)=kx,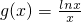
(1)求函数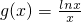 的单调递增区间;
的单调递增区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求k的取值范围;
(3)求证: .
.
解:(1)∵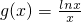 (x>0),∴
(x>0),∴ ,令g'(x)>0,得0<x<e,
,令g'(x)>0,得0<x<e,
故函数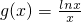 的单调递增区间为(0,e).
的单调递增区间为(0,e).
(2)由 ,则问题转化为k大于等于h(x)的最大值.
,则问题转化为k大于等于h(x)的最大值.
又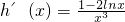 ,令
,令 .
.
当x在区间(0,+∞)内变化时,h'(x)、h(x)变化情况如下表:
由表知当 时,函数h(x)有最大值,且最大值为
时,函数h(x)有最大值,且最大值为 ,因此k≥
,因此k≥ .
.
(3)由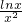 ≤
≤ ,∴
,∴ <
< (x≥2),
(x≥2),
∴ <
< .
.
又∵ <
< =
=
1- +
+ +
+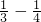 +…+
+…+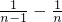 =1-
=1- <1,
<1,
∴ <
< .
.
分析:(1)由g'(x)>0,解得x的范围,就是函数的增区间.
(2)问题转化为k大于等于h(x)的最大值,利用导数求得函数h(x)有最大值,且最大值为 ,得到 k≥
,得到 k≥ .
.
(3)先判断 <
< (x≥2),得
(x≥2),得  <
< ,
,
用放缩法证明 <1,即得要证的不等式.
<1,即得要证的不等式.
点评:本题考查利用导数研究函数的单调性,求函数极值,用放缩法证明不等式,放缩不等式是解题的难点.
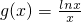 (x>0),∴
(x>0),∴ ,令g'(x)>0,得0<x<e,
,令g'(x)>0,得0<x<e,故函数
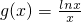 的单调递增区间为(0,e).
的单调递增区间为(0,e).(2)由
 ,则问题转化为k大于等于h(x)的最大值.
,则问题转化为k大于等于h(x)的最大值.又
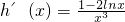 ,令
,令 .
.当x在区间(0,+∞)内变化时,h'(x)、h(x)变化情况如下表:
| x | (0, ) ) |  | ( ,+∞) ,+∞) |
| h'(x) | + | 0 | - |
| h(x) | ↗ |  | ↘ |
 时,函数h(x)有最大值,且最大值为
时,函数h(x)有最大值,且最大值为 ,因此k≥
,因此k≥ .
.(3)由
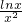 ≤
≤ ,∴
,∴ <
< (x≥2),
(x≥2),∴
 <
< .
.又∵
 <
< =
=1-
 +
+ +
+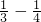 +…+
+…+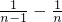 =1-
=1- <1,
<1,∴
 <
< .
.分析:(1)由g'(x)>0,解得x的范围,就是函数的增区间.
(2)问题转化为k大于等于h(x)的最大值,利用导数求得函数h(x)有最大值,且最大值为
 ,得到 k≥
,得到 k≥ .
.(3)先判断
 <
< (x≥2),得
(x≥2),得  <
< ,
,用放缩法证明
 <1,即得要证的不等式.
<1,即得要证的不等式.点评:本题考查利用导数研究函数的单调性,求函数极值,用放缩法证明不等式,放缩不等式是解题的难点.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目