题目内容
已知函数f（x）=(
)|x-1|，g（x）=x2-2ax+2，x∈[1，3]，对于?m∈R，均能在区间[1，3]内找到两个不同的n，使f（m）=g（n），则实数a的值是
| 1 | 2 |
2
2
．分析：由f（x）=(
)|x-1|=
，作出f（x）的图象，由g（x）=x2-2ax+2是开口向上，对称轴为x=a的抛物线，结合题设条件能求出a的值．
| 1 |
| 2 |
|
解答：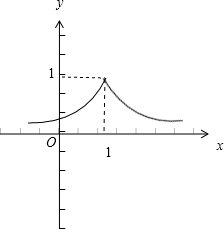
解：∵f（x）=(
)|x-1|=
，
∴f（x）的图象如图所示：
g（x）=x2-2ax+2是开口向上，对称轴为x=a的抛物线，
∵x∈[1，3]，对于?m∈R，均能在区间[1，3]内找到两个不同的n，使f（m）=g（n），
∴对称轴为x=a=
=2．
所以a=2．
故答案为：2．
解：∵f（x）=(| 1 |
| 2 |
|
∴f（x）的图象如图所示：
g（x）=x2-2ax+2是开口向上，对称轴为x=a的抛物线，
∵x∈[1，3]，对于?m∈R，均能在区间[1，3]内找到两个不同的n，使f（m）=g（n），
∴对称轴为x=a=
| 1+3 |
| 2 |
所以a=2．
故答案为：2．
点评：本题考查函数恒成立问题的合理运用，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|