题目内容
（本小题满分12分）
已知抛物线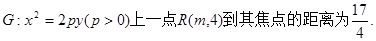
（I）求p与m的值；
（II）设抛物线G上一点P的横坐标t，过点P引斜率为—1的直线l交抛物线G于另一点A，交x轴于点B，若|OA|=|OB|（O为坐标原点），求点P的坐标。
【答案】
解：（Ⅰ）根据抛物线定义，点
到焦点的距离等于它到准线的距离，
即
，
解得
，
………………3分
∴抛物线方程为
，
点在抛物线上，得
，∴
。………………6分
（Ⅱ）点
,直线l的方程为
，
令
得
，则
。 ………………7分
联立方程
整理得
，
注意到方程已有一根
，求得方程的另一根
，
则
。
………………9分
，
，
∵
，∴
，
………………10分
得
，解得
。
点P的坐标为(
，1)。
………………12分
【解析】略
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
