题目内容
已知△ABC中,sinA+cosA= ,
,(1)求sinAcosA;
(2)求sinA-cosA;
(3)判断△ABC为锐角三角形还是钝角三角形.
【答案】分析:利用三角函数的基本性质进行化简并结合与三角形的关系进行求解.
解答:解:∵(sinA+cosA)2=( )2
)2
即1+2sinAcosA=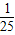
∴sinAcosA=-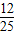
∵A是三角形ABC中的角,且sinAcosA<0
∴A位于第三象限
即△ABC是钝角三角形且sinA>0,cosA<0
∴1-2sinAcosA=(sinA-cosA)2=1+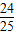
sinA-cosA=
故答案为:
(1)sinAcosA=-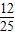
(2)sinA-cosA=
(3)△ABC是钝角三角形
点评:考察三角函数的化简以及在三角形中的应用,属于基础题.
解答:解:∵(sinA+cosA)2=(
 )2
)2即1+2sinAcosA=
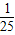
∴sinAcosA=-
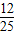
∵A是三角形ABC中的角,且sinAcosA<0
∴A位于第三象限
即△ABC是钝角三角形且sinA>0,cosA<0
∴1-2sinAcosA=(sinA-cosA)2=1+
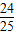
sinA-cosA=

故答案为:
(1)sinAcosA=-
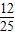
(2)sinA-cosA=

(3)△ABC是钝角三角形
点评:考察三角函数的化简以及在三角形中的应用,属于基础题.

练习册系列答案
相关题目
已知△ABC中,sinA:sinB:sinC=k:(k+1):2k (k≠0),则k的取值范围为( )
| A、(2,+∞) | ||
| B、(0,2) | ||
C、(
| ||
D、(
|